天池-新闻文本分类task0：任务简介

task1:机器学习算法
用TF-IDF作为文档向量，分类器分别使用了岭回归、朴素贝叶斯、SVM、随机森林、Xgboost和lightGBM。
关于集成学习中的随机森林、Xgboost和lightGBM可以参考我在CSDN的帖子《集成学习4：整理总结》

task2：fasttext
参考帖子：《学习笔记四：word2vec和fasttext》

task3：bert
参考帖子《天池入门赛-新闻文本分类-单个bert模型分数0.961》

一、赛事说明

比赛官方链接为：《零基础入门NLP - 新闻文本分类》。
讨论区有大佬张帆、惊鹊和张贤等人的代码，值得大家仔细阅读。
最后我的模型参考了这些代码的一些config，比如bert.config，lr等等。然后大佬们的代码对我来说还是太复杂，pytorch功力不够，看的吃力。所以参考HF主页的教程，自己用huggingface实现了。
1.1 数据标签
处理后的赛题训练数据如下：

在数据集中标签的对应的关系如下：{‘科技’: 0, ‘股票’: 1, ‘体育’: 2, ‘娱乐’: 3, ‘时政’: 4, ‘社会’: 5, ‘教育’: 6, ‘财经’: 7, ‘家居’: 8, ‘游戏’: 9, ‘房产’: 10, ‘时尚’: 11, ‘彩票’: 12, ‘星座’: 13}

评测指标为f1分数。

1.2 数据读取与数据分析

使用Pandas完成数据读取的操作：

import pandas as pd
train_df = pd.read_csv('../data/train_set.csv', sep='\t', nrows=100)
train_df.head()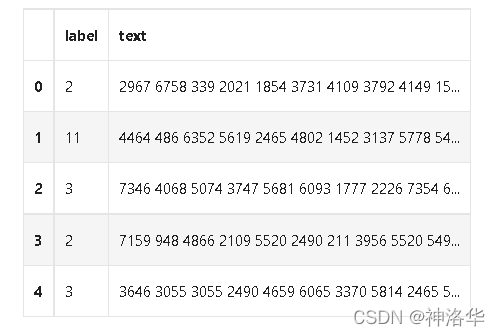

在这里插入图片描述

句子长度分析：
在赛题数据中每行句子的字符使用空格进行隔开，所以可以直接统计单词的个数来得到每个句子的长度。统计并如下：

%pylab inline
train_df['text_len'] = train_df['text'].apply(lambda x: len(x.split(' ')))
print(train_df['text_len'].describe())

Populating the interactive namespace from numpy and matplotlib
count     100.000000
mean      872.320000
std       923.138191
min        64.000000
25%       359.500000
50%       598.000000
75%      1058.000000
max      7125.000000
Name: text_len, dtype: float64

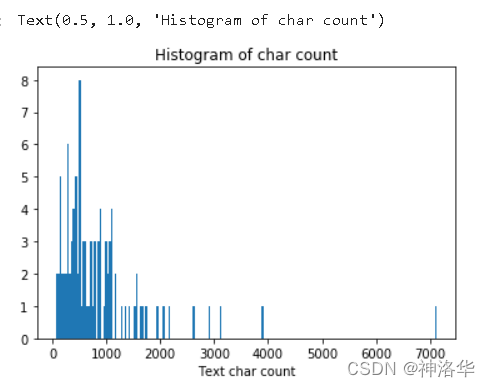
对新闻句子的统计可以得出，本次赛题给定的文本比较长，每个句子平均由907个字符构成，最短的句子长度为2，最长的句子长度为57921。

下图将句子长度绘制了直方图，可见大部分句子的长度都几种在2000以内。

_ = plt.hist(train_df['text_len'], bins=200)
plt.xlabel('Text char count')
plt.title("Histogram of char count")

在这里插入图片描述

新闻类别分布
接下来可以对数据集的类别进行分布统计，具体统计每类新闻的样本个数

train_df['label'].value_counts().plot(kind='bar')
plt.title('News class count')
plt.xlabel("category")

在这里插入图片描述
从统计结果可以看出，赛题的数据集类别分布存在较为不均匀的情况。在训练集中科技类新闻最多，其次是股票类新闻，最少的新闻是星座新闻。

字符分布统计
接下来可以统计每个字符出现的次数，首先可以将训练集中所有的句子进行拼接进而划分为字符，并统计每个字符的个数。

从统计结果中可以看出，在训练集中总共包括6869个字，其中编号3750的字出现的次数最多，编号3133的字出现的次数最少。

from collections import Counter
all_lines = ' '.join(list(train_df['text']))
word_count = Counter(all_lines.split(" "))
word_count = sorted(word_count.items(), key=lambda d:d[1], reverse = True)

print(len(word_count))

print(word_count[0])

print(word_count[-1])

2405
('3750', 3702)
('5034', 1)

这里还可以根据字在每个句子的出现情况，反推出标点符号。下面代码统计了不同字符在句子中出现的次数，其中字符3750，字符900和字符648在20w新闻的覆盖率接近99%，很有可能是标点符号。

from collections import Counter
train_df['text_unique'] = train_df['text'].apply(lambda x: ' '.join(list(set(x.split(' ')))))
all_lines = ' '.join(list(train_df['text_unique']))
word_count = Counter(all_lines.split(" "))
word_count = sorted(word_count.items(), key=lambda d:int(d[1]), reverse = True)

print(word_count[0])
print(word_count[1])
print(word_count[2])

('900', 99)
('3750', 99)
('648', 96)

数据分析的结论
通过上述分析我们可以得出以下结论：

赛题中每个新闻包含的字符个数平均为1000个，还有一些新闻字符较长；
赛题中新闻类别分布不均匀，科技类新闻样本量接近4w，星座类新闻样本量不到1k；
赛题总共包括7000-8000个字符；

通过数据分析，我们还可以得出以下结论：

每个新闻平均字符个数较多，可能需要截断；
由于类别不均衡，会严重影响模型的精度；
二、task1:机器学习算法
用TF-IDF作为文档向量，分类器分别使用了岭回归、朴素贝叶斯、SVM、随机森林、Xgboost和lightGBM。
关于集成学习中的随机森林、Xgboost和lightGBM可以参考我在CSDN的帖子《集成学习4：整理总结》
1.1 bagging
Bagging：通过Bootstrap 的方式对全样本数据集进行抽样得到抽样子集，对不同的子集使用同一种基本模型进行拟合，然后投票得出最终的预测。Bagging主要通过降低方差的方式减少预测误差

Bagging的一个典型应用是随机森林。由许多“树”bagging组成的。每个决策树训练的样本和构建决策树的特征都是通过随机采样得到的，随机森林的预测结果是多个决策树输出的组合（投票）

1.2 boosting

使用同一组数据集进行反复学习，得到一系列简单模型，然后组合这些模型构成一个预测性能十分强大的机器学习模型。

Boosting通过不断减少偏差的形式提高最终的预测效果，与Bagging有着本质的不同。

1.3 Adaboost算法原理

不改变训练数据，而是改变其权值分布，使每一轮的基学习器学习不同权重分布的样本集，最后加权组合表决组合。

Adaboost算法是由基本分类器组成的加法模型，损失函数为指数损失函数。

用前向分布算法，从指数损失函数推导出分类错误率$e{m}$、分类器$G_m(x)$的权重系数$\alpha{m}$、样本权重更新公式。每轮学习时提高那些被前一轮分类器错误分类的样本的权重，来改变数据的概率分布。

分类误差率 $e_{m}=\\sum_{i=1}^{N} P\\left(G_{m}\\left(x_{i}\\right) \\neq y_{i}\\right)=\\sum_{i=1}^{N} w_{m i} I\\left(G_{m}\\left(x_{i}\\right) \\neq y_{i}\\right)$
分类器$Gm(x)$的权重系数$\alpha{m}=\frac{1}{2} \log \frac{1-e{m}}{e{m}}$ $\\alpha_{m}=\\frac{1}{2} \\log \\frac{1-e_{m}}{e_{m}}$
权重分布 $\\begin{array}{c} D_{m+1}=\\left(w_{m+1,1}, \\cdots, w_{m+1, i}, \\cdots, w_{m+1, N}\\right) \\\\\ w_{m+1, i}=\\frac{w_{m i}}{Z_{m}} \\exp \\left(-\\alpha_{m} y_{i} G_{m}\\left(x_{i}\\right)\\right), \\quad i=1,2, \\cdots, N, \\end{array}\$
基本分类器加权组合表决 $\ \\begin{aligned} G(x) &=\\operatorname{sign}(f(x)) \\\\ &=\\operatorname{sign}\\left(\\sum_{m=1}^{M} \\alpha_{m} G_{m}(x)\\right)\ \\end{aligned}\$ $sign(x)=\\begin{cases} 1 & \\text{ if } x\\ geqslant 0 \\\\ -1 & \\text{ if } x< 0 \\end{cases}$
1.4 GBDT

GBDT 的全称是 Gradient Boosting Decision Tree，梯度提升树。GBDT使用的决策树是CART回归树。因为GBDT每次迭代要拟合的是梯度值，是连续值所以要用回归树。
回归问题没有分类错误率可言，用每个样本的残差表示每次使用基函数预测时没有解决的那部分问题。

GBDT和Adaboost区别：

拟合思路

Adaboost算法：使用了分类错误率修正样本权重以及计算每个基本分类器的权重。通过不断修改样本权重（增大分错样本权重，降低分对样本权重），不断加入弱分类器进行boosting。
GBDT：拟合残差来学习基模型。残差定义为损失函数相对于前一轮组合树模型的负梯度方向的值作为残差的近似值（损失函数的负梯度在当前模型的值）

除了均方差损失函数时，负梯度值等于残差。

GBDT 的每一步残差计算其实变相地增大了被分错样本的权重，而对与分对样本的权重趋于 0，这样后面的树就能专注于那些被分错的样本。
Adaboost是分类树，GBDT是回归树，但是也可以做分类。
损失函数不同。基于残差 GBDT 容易对异常值敏感，所以一般回归类的损失函数会用绝对损失或者 Huber 损失函数来代替平方损失函数。
1.5 XGBoost
XGBoost 是 Boosting 框架的一种实现结构， lightgbm 也是一种框架实现结构，而 GBDT 则是一种算法实现。XGBoost本质也是GBDT，相比于 GBDT 的差别主要就是 XGBoost 做的优化。
构造目标函数为：
使用泰勒级数近似目标函数：

对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶导数。并在代价函数里加入了正则项，用于控制模型的复杂度，使学习出来的模型更加简单，防止过拟合

模型复杂度$\Omega\left(f{K}\right)$，它可以由叶子节点的个数以及节点函数值来构建，则：$\Omega\left(f{K}\right) = \gamma T+\frac{1}{2} \lambda \sum{j=1}^{T} w{j}^{2}$ 。
分割节点的标准为$max\{\tilde{\mathcal{L}}^{(old)} - \tilde{\mathcal{L}}^{(new)} \}$，为了找到找到最优特征及最优切分点，有三种策略：
- 精确贪心分裂算法：首先找到所有的候选特征及所有的候选切分点, 求其 $\mathcal{L}{\text {split }}$, 然后选择使$\mathcal{L}{\mathrm{split}}$ 最大的特征及对应切分点作为最优特征和最优切分点。节点分裂时只选择当前最优的分裂策略, 而非全局最优的分裂策略。

支持列抽样和缺失值处理。x列抽样，不仅能降低过拟合，还能减少计算，这也是xgboost异于传统gbdt的一个特性。对于特征的值有缺失的样本，xgboost可以自动学习出它的分裂方向（稀疏感知算法）。

XGBoost缺点：

虽然利用预排序和近似算法可以降低寻找最佳分裂点的计算量，但在节点分裂过程中仍需要遍历数据集；
预排序过程的空间复杂度过高，不仅需要存储特征值，还需要存储特征对应样本的梯度统计值的索引，相当于消耗了两倍的内存

1.6 LightGBM

轻量级（Light）的梯度提升机（GBM），主要用于解决 GDBT 在海量数据中遇到的问题。其相对 XGBoost 具有训练速度快、内存占用低的特点。
LightGBM 为了解决XGBoost的问题提出了以下几点解决方案：

单边梯度抽样算法；
直方图算法；
互斥特征捆绑算法；
。。。

单边梯度抽样算法：

梯度大小可以反应样本的权重，梯度越小说明模型拟合的越好。单边梯度抽样算法（Gradient-based One-Side Sampling, GOSS）保留了梯度大的样本，并对梯度小的样本进行随机抽样，减少了大量梯度小的样本，极大的减少了计算量。(在接下来的计算锅中只需关注梯度高的样本)
为了不改变样本的数据分布，在计算增益时为梯度小的样本引入一个常数进行平衡。

一、赛事说明

1.1 数据标签

1.2 数据读取与数据分析

二、task1:机器学习算法

1.1 bagging

1.2 boosting

1.3 Adaboost算法原理

1.4 GBDT

1.5 XGBoost

1.6 LightGBM