一、RNN

前馈神经网络：信息往一个方向流动。包括MLP和CNN
循环神经网络：信息循环流动，网络隐含层输出又作为自身输入</font>，包括RNN、LSTM、GAN等。

1.1 RNN模型结构

RNN模型结构如下图所示：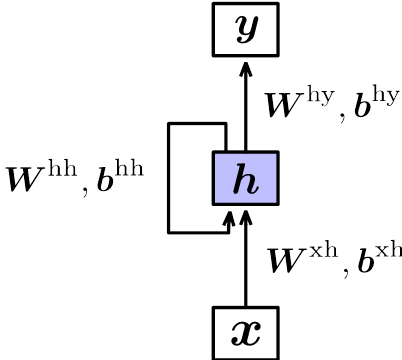

展开之后相当于堆叠多个共享隐含层参数的前馈神经网络：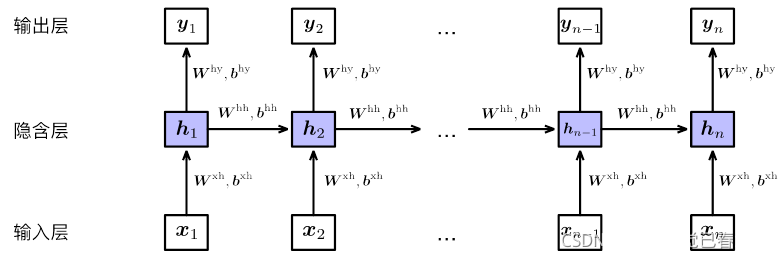

其输出为：

$$\mathbf {h_{t}=tanh(W^{xh}x_{t}+b^{xh}+W^{hh}h_{t-1}+b^{hh})}$$ $$\mathbf {y_{n}=softmax(W^{hy}h_{n}+b^{hy})}$$

• 隐含层输入不但与当前时刻输入$x{t}$有关，还与前一时刻隐含层$h{t-1}$有关。每个时刻的输入经过层层递归，对最终输入产生一定影响。
• 每个时刻隐含层$h_{t}$包含1~t时刻全部输入信息，所以隐含层也叫记忆单元（Memory）
• 每个时刻参数共享（‘循环’的由来）</font>
• 使用tanh激活函数是因为值域（-1,1），能提供的信息比sigmoid、Relu函数丰富。
• 变长神经网络只能进行层标准化
• RNN处理时序信息能力很强，可以用于语音处理。NLP等

  1.2 RNN模型的缺点

  在前向传播时： $$\mathbf {h_{t}=tanh(W^{xh}x_{t}+b^{xh}+W^{hh}h_{t-1}+b^{hh})}$$ 假设最后时刻为t，反向传播求对i时刻的导数为： $$\mathbf {\frac{\partial Loss}{\partial W_{i}^{hh}}=\frac{\partial Loss}{\partial y_{t}^{}}\cdot \frac{\partial y_{t}^{}}{\partial h_{i}}\cdot \frac{\partial h_{i}^{}}{\partial W_{i}^{hh}}}$$ $$\mathbf {\frac{\partial h_{i}}{\partial W_{i}^{hh}}=(h_{i-1})^T}$$ $$\mathbf {\frac{\partial y_{t}}{\partial h_{i}}=\frac{\partial y_{t}}{\partial h_{t}}\cdot\frac{\partial h_{t}}{\partial h_{i}}=\frac{\partial y_{t}}{\partial h_{t}}\cdot tanh'\cdot\frac{\partial h_{t}}{\partial (h_{t-1})^{T}}\cdot\tanh'\cdot\frac{\partial h_{t-1}}{\partial (h_{t-2})^{T}}...\cdot\tanh'\cdot\frac{\partial h_{i+1}}{\partial (h_{i})^{T}}=\frac{\partial y_{t}}{\partial h_{t}}\cdot (tanh')^{t-i}\cdot W^{t-i}}$$ 所以最终结果是：$\mathbf {\frac{\partial Loss}{\partial W_{i}^{hh}}=\frac{\partial Loss}{\partial y_{t}}\cdot\frac{\partial y_{t}}{\partial h_{t}}\cdot (tanh')^{t-i}\cdot W^{t-i}\cdot(h_{i-1})^T}$
  可以看到涉及到矩阵W的连乘。

线性代数中有：$W=P^{-1}\Sigma P$
其中，$E=P^{-1} P$为单位矩阵，$\Sigma$为对角线矩阵，对角线元素为W对应的特征值。即

$$\Sigma =\begin{bmatrix} \lambda _{1} & ... & 0\\ ... &... &... \\ ... & ... &\lambda _{m} \end{bmatrix}$$

所以有：

$$W=P^{-1}\Sigma^T P=\Sigma =\begin{bmatrix} \lambda _{1}^T & ... & 0\\ ... &... &... \\ ... & ... &\lambda _{m} ^T \end{bmatrix}$$

所以有：

1. 矩阵特征值$\lambda _{m}$要么大于1要么小于1。所以t时刻导数要么梯度消失，要么梯度爆炸。而且比DNN更严重。</font>因为DNN链式求导累乘的各个W是不一样的，有的大有的小，互相还可以抵消影响。而RNN的W全都一样，必然更快的梯度消失或者爆炸。
2. $\lambda {m}>1$则$\lambda {m}^T→\infty$，过去信息越来越强，$\lambda {m}＜1$则$\lambda {m}^T→0$，信息原来越弱，传不远。所有时刻W都相同，即所有时刻传递信息的强度都一样，传递的信息无法调整，和当前时刻输入没太大关系。
3. 为了避免以上问题，序列不能太长。
4. 无法解决超长依赖问题：例如$h1$传到$h{10}$，$x_1$的信息在中间被多个W和$x_2-x_9$稀释
5. 递归模型，无法并行计算

二、长短时记忆网络LSTM

RNN的缺点是信息经过多个隐含层传递到输出层，会导致信息损失。更本质地，会造成网络参数难以优化。LSTM加入全局信息context，可以解决这一问题。

2.1 LSTM模型结构

1. 跨层连接</font>
   LSTM首先将隐含层更新方式改为： $$\mathbf {u_{t}=tanh(W^{xh}x_{t}+b^{xh}+W^{hh}h_{t-1}+b^{hh})}$$ $$\mathbf {h_{t}=h_{t-1}+u_{t}}$$

这样可以直接将$h{k}$与$h{t}$相连，实现跨层连接，减小网络层数，使得网络参数更容易被优化。</font>证明如下：

$$\mathbf {h_{t}=h_{t-1}+u_{t}=h_{t-2}+u_{t-1}+u_{t}=...=h_{k}+u_{k+1}+u_{k+2}+...+u_{t-1}+u_{t}}$$

1. 增加遗忘门 forget gate</font>
   上式直接将旧状态$h{t-1}$和新状态$u{t}$相加，没有考虑两种状态对$h{t}$的不同贡献。故计算$h{t-1}$和$u_{t}$的系数，再进行加权求和</font> $$\mathbf {f_{t}=\sigma(W^{f,xh}x_{t}+b^{f,xh}+W^{f,hh}h_{t-1}+b^{f,hh})}$$ $$\mathsf {h_{t}=f_{t}\odot h_{t-1}+(1-f_{t})\odot u_{t}}$$ 其中$\sigma$表示sigmoid函数，值域为（0，1）。当$f_{t}$较小时，旧状态贡献也较小，甚至为0，表示遗忘不重要的信息，所以称为遗忘门。
2. 增加输入门 Input gate</font>
   上一步问题是旧状态$h{t-1}$和新状态$u{t}$权重互斥。但是二者可能都很大或者很小。所以需要用独立的系数来调整。即： $$\mathbf {i_{t}=\sigma(W^{i,xh}x_{t}+b^{i,xh}+W^{i,hh}h_{t-1}+b^{i,hh})}$$ $$\mathsf {h_{t}=f_{t}\odot h_{t-1}+i_{t}\odot u_{t}}$$ $i{t}$用于控制输入状态$u{t}$对当前状态的贡献，所以称为输入门
3. 增加输出门output gate</font> $$\mathbf {o_{t}=\sigma(W^{o,xh}x_{t}+b^{o,xh}+W^{o,hh}h_{t-1}+b^{o,hh})}$$
4. 综合计算 $$\mathbf {u_{t}=tanh(W^{xh}x_{t}+b^{xh}+W^{hh}h_{t-1}+b^{hh})}$$ $$\mathbf {f_{t}=\sigma(W^{f,xh}x_{t}+b^{f,xh}+W^{f,hh}h_{t-1}+b^{f,hh})}$$ $$\mathbf {i_{t}=\sigma(W^{i,xh}x_{t}+b^{i,xh}+W^{i,hh}h_{t-1}+b^{i,hh})}$$ $$\mathbf {c_{t}=f_{t}\odot c_{t-1}+i_{t}\odot u_{t}}$$ $$\mathbf {h_{t}=o_{t}\odot tanh(c_{t})}$$ $$\mathbf {y_{n}=softmax(W^{hy}h_{n}+b^{hy})}$$

• 遗忘门：$f{t}$，是$c{t-1}$的系数，可以过滤上一时刻的记忆信息。否则之前时刻的$ct$完全保留，$c_t$越来越大，$\mathbf {h{t}=o{t}\odot tanh(c{t})}$tanh会马上饱和，无法输入新的信息。
• 输入门：$i{t}$，是$u{t}$的系数，可以过滤当前时刻的输入信息。即不会完整传递当前输入信息，可以过滤噪声等
• 输出门：$o{t}$，是$tanh(c{t})$的系数，过滤记忆信息。即$c_t$一部分与当前分类有关，部分是与当前分类无关信息，只是用来传递至未来时刻
• 三个门控单元，过滤多少记住多少，都跟前一时刻隐含层输出和当前时刻输入有关
• 记忆细胞：$c_{t}$，记录了截止当前时刻的重要信息。

可以看出RNN的输入层隐含层和输出层三层都是共享参数，到了LSTM都变成参数不共享了。

2.2 双向循环神经网络Bi-LSTM

• 解决循环神经网络信息单向流动的问题。（比如一个词的词性与前面的词有关，也与自身及后面的词有关）
• 将同一个输入序列分别接入前向和后向两个循环神经网络中，再将两个循环神经网络的隐含层结果拼接在一起，共同接入输出层进行预测。其结构如下：
  
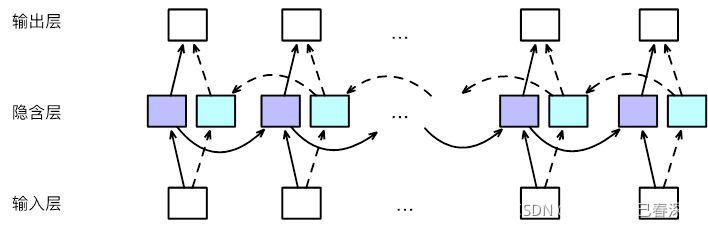
  此外还可以堆叠多个双向循环神经网络。
  LSTM比起RNN多了最后时刻的记忆细胞，即：

bilstm=nn.LSTM(
        input_size=1024, 
        hidden_size=512, 
        batch_first=True,
        num_layers=2,#堆叠层数
        dropout=0.5,  
        bidirectional=True#双向循环)

hidden, hn = self.rnn(inputs)
#hidden是各时刻的隐含层，hn为最后时刻隐含层
hidden, (hn, cn) = self.lstm(inputs)
#hidden是各时刻的隐含层，hn, cn为最后时刻隐含层和记忆细胞

三、序列到序列模型

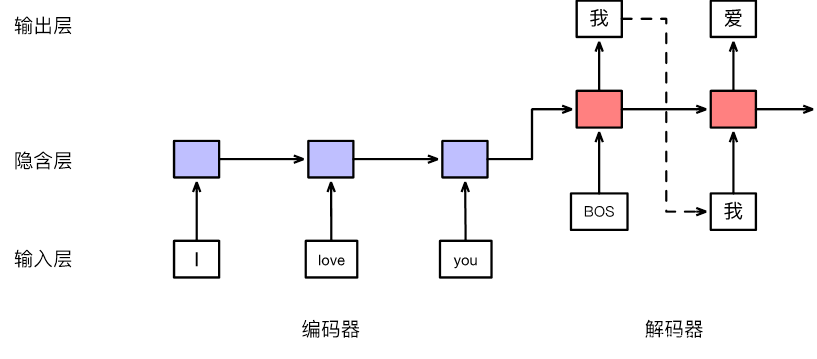
encoder最后状态的输出输入decoder作为其第一个隐含状态$h_0$。decoder每时刻的输出都会加入下一个时刻的输入序列，一起预测下一时刻的输出，直到预测出End结束。