@[toc]
一、字符串基础
1.1 字符串基础知识
1.1.1 字符串简介
- 字符串的表示:字符串是由0个或多个字符组成的有序字符序列,由一对单引号或一对双引号表示
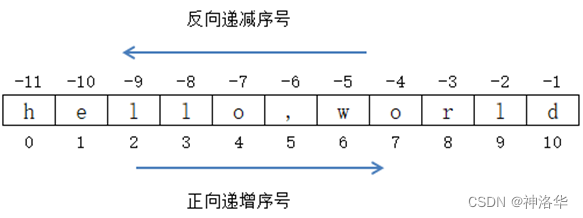
- 字符串有2类共4种表示方法:
- 由1对单引号或双引号表示,仅表示单行字符串;
- 由1对三单引号或三双引号表示,可表示多行字符串;
字符串是字符的有序序列,可以对其中的字符进行索引。
特殊字符:使用转义符
\,\b表示回退;\n表换行(光标移动到下行首;\r表示回车(光标移动到本行首),\t表示制表符(4格)1.1.2 字符串处理
- 字符串操作符
| 操作符及查找 | 描述 |
|---|---|
x+y |连接两个字符串x和y
nx或xn | 复制n次字符串x
x in s |如果x是s的子串,返回True,否则返回False
str.index(‘’) |子串第一次出现的位置,不存在报错ValueError
str.rindex(‘’) |子串最后一次出现的位置,不存在报错ValueError
str.find(‘’) |子串第一次出现的位置,不存在返回-1
str.rfind(‘’)| 子串最后一次出现的位置,不存在返回-1
- 字符串处理函数
函数及使用| 描述
|—|—|
len(x) |返回字符串的长度,非空字符串都有长度(换行符、空格和符号长度1)
str(x) |将x转换为string类型
hex(x)或oct(x) |将整数x转换成16进制或8进制字符串
chr(x) |将一个(0-255)10或16进制整数(Unicode编码),转换成对应ASCII字符
ord(x) |x为字符,返回其对应的Unicode编码(原始值0-65535)
- 字符串大小写
大小写转换| 描述
|—|—|
str.lower()或str.upper() | 全部字符小写或大写,产生新字符串
str.swapcase() |字符串大写改小写,小写改大写,产生新字符串
str.capitalize()| 首字符大写,其余小写,产生新字符串
str.title() |每个字符首字符大写,其余小写,产生新字符串
- 字符串对齐
字符串对齐| 描述
|—|—|
str.center(width,’stp’)| 居中对齐,width指定宽度,stp指定分隔符,默认空格分割。
str.ljust(width,’stp’)| 左对齐,width指定宽度,stp指定分隔符,默认空格分割。
str.rjust(width,’stp’)| 右对齐,width指定宽度,stp指定分隔符,默认空格分割。
str.zfill(width)| 右对齐,左侧用0填充,width指定宽度。
以上对齐方式,指定宽度小于实际宽度时返回原字符串
- 字符串处理函数
函数及使用| 描述
|—|—|
str.split(‘sep’,maxsplit) |从str左侧开始分割,分隔符为sep,默认空格。第二个参数指定最大分割次数。最大分割后剩余字符串成一个元素
str.rsplit(‘sep’,maxsplit)| 同上,从右侧开始分割。直接写’/’或者sep=’/’都可以。最大分割后的元素不同。没有指定最大分割时是一样的
str.count(sub)| 返回子串sub在str中的出现的次数
str.replace(old,new,num)| 返回字符串str副本,所有old子串被替换为new,num为最大替换次数
str.center(width[,fillchar])| 字符串str根据宽度width居中,fillchar可选填
str.strip(chars)| 从str中去掉在其左侧和右侧chars中列出的字符
str.join(iter)| 在iter变量除最后元素外每个元素后增加一个str
str.isidentifier() |判断字符串是否是合法标识符(汉字也算)
str.isspace() |判断字符串是否都是由空白字符组成(回车、换行、水平制表符)
str.isalpha() |判断字符串是否都是由字母组成(汉字也算)
str.isdecimal()| 判断字符串是否都是由十进制数字组成
str.isnumeric()| 判断字符串是否都是由数字组成(包括罗马数字)
str.isalnum() |判断字符串是否都是由数字和字母组成
- 字符串的比较
字符串可以用<、>、=、>=、<=、==、!=来比较。比较原理是比较每个字符的原始值(unicode编码),可用ord查看 编码与解码
- 编码:将字符串转换成二进制数据(byte)(gbk中文两个字节,utf-8中文三个字节)
- 格式:
str.encode(encoding=’gbk’)(gbk大小写都可以,开头b表二进制) - 解码:将二进制数据(byte)转换成字符串
- 格式:
byte.decode((encoding=’gbk’)(byte为二进制编码),解码格式应该与编码格式一致1.1.3 字符串类型的格式化
字符串格式化有两种方式:- 用%占位输出
如print(‘我是%s,今年%d岁,%(name,age))
print(‘我今年%10.2f岁’ % age)
结果:我是name,今年age岁 - 用{}输出,如
print(f‘我是(name),今年(age)岁)
print(‘我是{0},今年{1}岁’.format(name,age))(槽中0 和1可以不写)
- 用%占位输出
整数类型输出格式:
- b:输出整数的二进制方式
- c:输出整数对应的Unicode字符
- d:输出整数的十进制方式
- o:输出整数的八进制方式
- x:输出整数的小写十六进制方式
- X:输出整数的大写十六进制方式
浮点数类型输出格式:
- e:输出浮点数对应的小写字母e的指数形式
- E:输出浮点数对应的大写字母E的指数形式
- f:输出浮点数的标准浮点形式
- %:输出浮点数的百分比形式
- {:.2f}表示小数点后两位的小数
- {:.2}表示一共两位数,有十位时表示为3e+01的形式
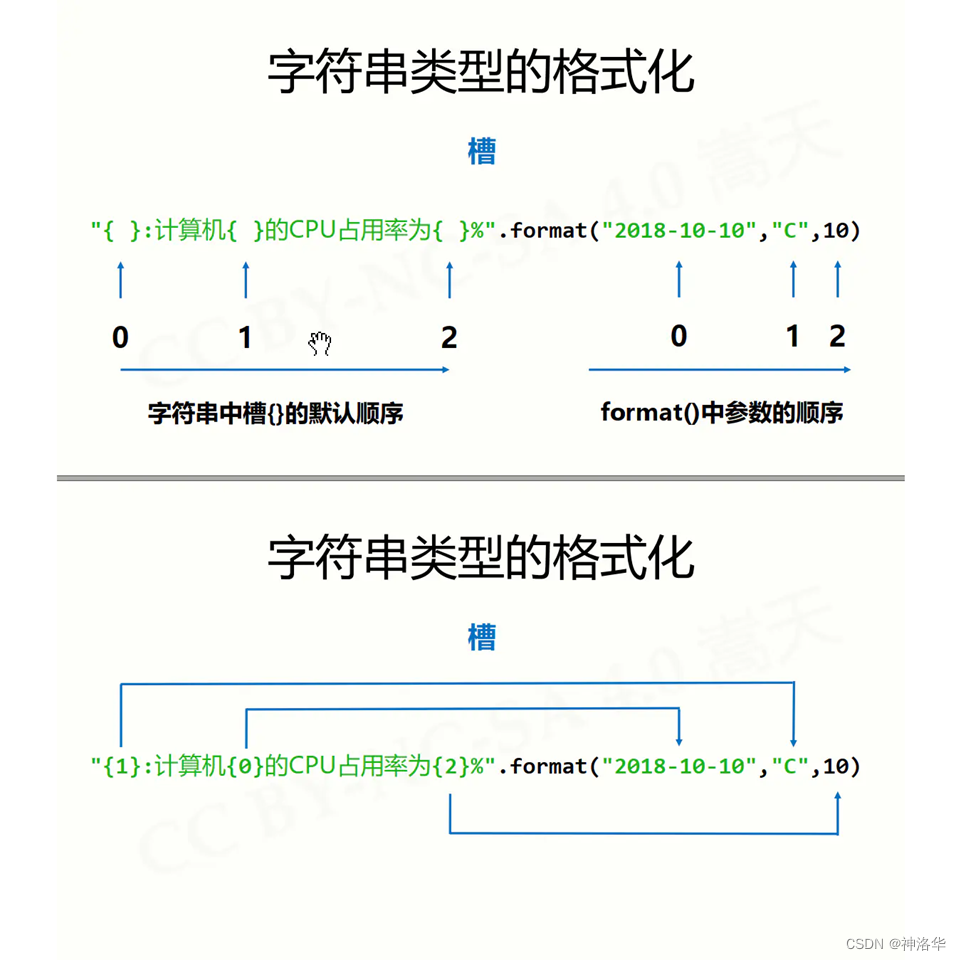
②格式控制

1.2 字符串基础题目
1.2.1 字符串基础题目列表
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 0125 | 验证回文串 | Python | 字符串、双指针 | 简单 |
| 0005 | 最长回文子串 | Python | 字符串、动态规划 | 中等 |
| 0003 | 无重复字符的最长子串 | Python | 字符串、哈希表、双指针、字符串、滑动窗口 | 中等 |
| 0344 | 反转字符串 | Python | 字符串 | 简单 |
| 0557 | 反转字符串中的单词 III | Python | 字符串 | 简单 |
| 0049 | 字母异位词分组 | Python | 字符串、哈希表 | 中等 |
| 0415 | 字符串相加 | Python | 字符串、大数加法 | 简单 |
| 0151 | 颠倒字符串中的单词 | Python | 双指针、字符串 | 中等 |
| 0043 | 字符串相乘 | Python | 数学、字符串、模拟 | 中等 |
| 0014 | 最长公共前缀 | Python | 字符串 | 简单 |
1.2.2 验证回文串
如果将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。
给你一个字符串 s,如果它是 回文串 ,返回 true ;否则,返回 false 。
class Solution: |
作者:LeetCode-Solution
链接:https://leetcode.cn/problems/valid-palindrome/solution/yan-zheng-hui-wen-chuan-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1.2.3 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
输入:s = "babad" |
思路 1:动态规划
初始化一个
n * n大小的布尔类型数组dp[][],dp[i][j]表示字符串s上 从位置i到j的子串s[i...j]是否是一个回文串,下面进行判断:当子串只有
1位或2位的时候,如果s[i] == s[j],该子串为回文子串,dp[i][j] = (s[i] == s[j])。如果子串大于
2位,则如果s[i + 1...j - 1]是回文串,且s[i] == s[j],则s[i...j]也是回文串,dp[i][j] = (s[i] == s[j]) and dp[i + 1][j - 1]。
当判断完
s[i: j]是否为回文串时,判断并更新最长回文子串的起始位置和最大长度。
class Solution(object): |
1.2.4 无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
输入: s = "abcabcbb" |
class Solution(object): |
class Solution: |
1.2.5 字符串相加
给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回。
你不能使用任何內建的用于处理大整数的库(比如 BigInteger), 也不能直接将输入的字符串转换为整数形式。
解题思路:本题不能将字符串直接转为整数之后,在整数之间相加计算。只能对两个大整数模拟「竖式加法」的过程,如下所示:
算法流程:
- 设定
i,j两指针分别指向num1,num2尾部,模拟人工加法; - 计算进位: 计算
add= tmp // 10,代表当前位相加是否产生进位; - 添加当前位: 计算
tmp = n1 + n2 + add,即当前位的结果。但是这其中要除去进位,所以当前位实际结果是tmp % 10,将其添加至ans头部;(比如计算9+4=13,当前位计算结果是3,但是进位add=1,累积到高一位的计算中) - 索引溢出处理: 当指针
i或j走过数字首部后,给n1,n2赋值为0,相当于给num1,num2中长度较短的数字前面填 0,以便后续计算。 - 当遍历完
num1,num2后跳出循环,并根据add值决定是否在头部添加进位 1,最终返回 res 即可。这其中的关键点,就是用add来表示前一位是否对当前位产生了进位,并将这个进位状态不断累加到后续每一位的计算中。
class Solution:
def addStrings(self, num1: str, num2: str) -> str:
ans=""
i,j,add=len(num1)-1,len(num2)-1,0
while i>=0 or j>=0:# 只要有一个数还可以计算
#位数减为负则补0
n1=int(num1[i]) if i>=0 else 0
n2=int(num2[j]) if j>=0 else 0
temp=n1+n2+add # 当前位计算结果
add=temp//10 #判断是否要进一位
ans=str(temp%10)+ans # 当前位写入的结果
i-=1
j-=1
return "1"+ans if add==1 else ans1.2.6 字符串相乘
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
注意:不能使用任何内置的 BigInteger 库或直接将输入转换为整数。
输入: num1 = "123", num2 = "456" |
思路一:先算乘数的每一位相乘结果再相加
- 将较长的字符作为被乘数(
num1),较短的作为乘数(num2)。 - 遍历
num2的每一位j,将num2[j]乘以num1的每一位,得到结果ans - 将结果
ans存在列表ls中,最后再将ls的所有中间结果依次相加(借用上一题的相加函数)
比如996*32=1992+29980=31872。class Solution(object):
def multiply(self, num1, num2):
"""
:type num1: str
:type num2: str
:rtype: str
"""
if num1=='0' or num2=='0':
return '0' # 如果没有这一步,会算出'00000'之类的
# 将nums1设为更长的数
if len(num1)-1<len(num2)-1:
num1,num2=num2,num1
ls=[] # 记录nums2每一位和nums1相乘的结果
count=0 # 记录nums2的位数,每进一位中间结果要乘以10
for j in range(len(num2)-1,-1,-1):
n2=int(num2[j]) # 用nums2的每一位乘以nums1的所有位
add=0
ans=''
for i in range(len(num1)-1,-1,-1):
n1=int(num1[i])
#print(n1,n2)
temp=n1*n2+add
add=temp//10
ans=str(temp%10)+ans
ans=str(add)+ans if add!=0 else ans # 因为是相乘,进位可以是1到8(9*9=81)
ls.append(ans+'0'*count)
count+=1
#print(ls)
res='0'
for i in range(len(ls)):
res=self.addStrings(res,ls[i])
return res
def addStrings(self, num1, num2): # 加法函数
ans=""
i,j,add=len(num1)-1,len(num2)-1,0
while i>=0 or j>=0:# 只要有一个数还可以计算
#位数减为负则补0
n1=int(num1[i]) if i>=0 else 0
n2=int(num2[j]) if j>=0 else 0
temp=n1+n2+add # 当前位计算结果
add=temp//10 #判断是否要进一位
ans=str(temp%10)+ans # 当前位写入的结果
i-=1
j-=1
return "1"+ans if add==1 else ans
思路二:各位相乘后,再相加
长度为 len(num1) 的整数 num1 与长度为 len(num2) 的整数 num2 相乘的结果长度为 len(num1) + len(num2) - 1 或 len(num1) + len(num2)。所以我们可以使用长度为 len(num1) + len(num2) 的整数数组 nums 来存储两个整数相乘之后的结果。(相当于首位可能补了0,如果最终结果没有进位的话)
整个计算流程的步骤如下:
- 从个位数字由低位到高位开始遍历
num1,取得每一位数字digit1。从个位数字由低位到高位开始遍历num2,取得每一位数字digit2。 - 将
digit1 * digit2的结果累积存储到nums对应位置i + j + 1上。(比如1996*23时,nums=[0, 2, 21, 45, 39, 18]) - 从
len(num1) + len(num2) - 1的位置由低位到高位遍历数组nums。将每个数位上大于等于10的数字进行进位操作,然后对该位置上的数字进行取余操作。 - 最后判断首位是否有进位。如果首位为
0,则从第1个位置开始将答案数组拼接成字符串。如果首位不为0,则从第0个位置开始将答案数组拼接成字符串。并返回答案字符串。
class Solution: |
1.2.7 最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀,返回空字符串 ""。
思路一:纵向比较
从前往后遍历所有字符串的每一列,比较相同列上的字符是否相同,如果相同则继续对下一列进行比较,如果不相同则当前列不再属于公共前缀class Solution(object):
def longestCommonPrefix(self, strs):
"""
:type strs: List[str]
:rtype: str
"""
if not strs:
return ""
le=[len(x) for x in strs]
min_le=min(le) # 最短的长度
i=0
while i <min_le:
se=set(strs[0][i]) # 从第一个字符串的第一个字符开始比较
for ch in strs[1:]:
if ch[i] not in se:
return strs[0][:i]
i+=1
return strs[0][:i]
或者是:
class Solution: |
二、单模式串匹配算法
2.1 Brute Force 算法(暴力匹配)
2.1.1 算法介绍
- Brute Force 算法:简称为 BF 算法。中文意思是暴力匹配算法,也可以叫做朴素匹配算法。
- BF 算法思想:对于给定文本串
T与模式串p,从文本串的第一个字符开始与模式串p的第一个字符进行比较,如果相等,则继续逐个比较后续字符,否则从文本串T的第二个字符起重新和模式串p进行比较。依次类推,直到模式串p中每个字符依次与文本串T的一个连续子串相等,则模式匹配成功。否则模式匹配失败。
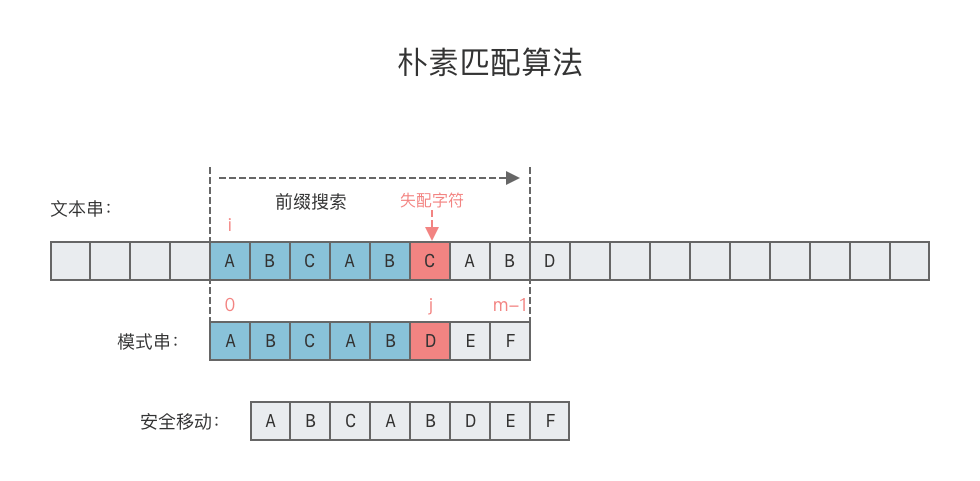
Brute Force 算法步骤
- 对于给定的文本串
T与模式串p,求出文本串T的长度为n,模式串p的长度为m。 - 同时遍历文本串
T和模式串p,先将T[0]与p[0]进行比较。- 如果相等,则继续比较
T[1]和p[1]。以此类推,一直到模式串p的末尾p[m - 1]为止。 - 如果不相等,则将文本串
T移动到上次匹配开始位置的下一个字符位置,模式串p则回退到开始位置,再依次进行比较。
- 如果相等,则继续比较
- 当遍历完文本串
T或者模式串p的时候停止搜索。
- 对于给定的文本串
2.1.2 代码实现
def bruteForce(T: str, p: str) -> int: |
2.2.3 算法分析
BF 算法非常简单,容易理解,但其效率很低。主要是因为在匹配过程中可能会出现回溯:当遇到一对字符不同时,模式串 p 直接回到开始位置,文本串也回到匹配开始位置的下一个位置,再重新开始比较。
最坏时间复杂度为 $O(m \times n)$。在回溯之后,文本串和模式串中一些部分的比较是没有必要的。由于这种操作策略,导致 BF 算法的效率很低。最坏情况是每一趟比较都在模式串的最后遇到了字符不匹配的情况,每轮比较需要进行
m次字符对比,总共需要进行n - m + 1轮比较,总的比较次数为m * (n - m + 1)。最佳时间复杂度是 $O(m)$。最理想的情况下(第一次匹配直接匹配成功)。
平均时间复杂度为 $O(n + m)$。在一般情况下,根据等概率原则,平均搜索次数为 $\frac{(n + m)}{2}$。
2.2 KMP 算法介绍
参考:
KMP 算法:全称叫做 「Knuth Morris Pratt 算法」,是由它的三位发明者 Donald Knuth、James H. Morris、 Vaughan Pratt 的名字来命名的。KMP 算法是他们三人在 1977 年联合发表的。
KMP 算法思想:对于给定文本串 T 与模式串 p,当发现文本串 T 的某个字符与模式串 p 不匹配的时候,可以利用匹配失败后的信息,尽量减少模式串与文本串的匹配次数,避免文本串位置的回退,以达到快速匹配的目的。
2.2.1 朴素匹配算法的缺陷
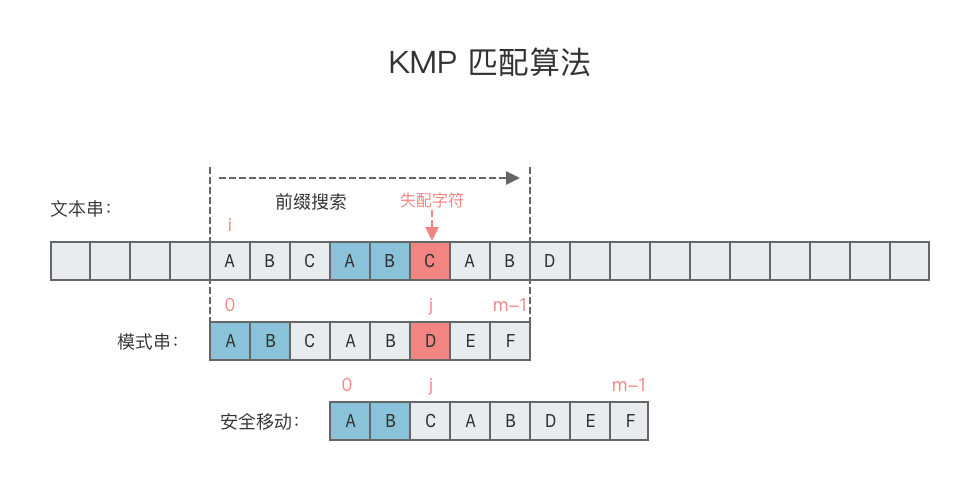
在朴素匹配算法的匹配过程中,我们分别用指针 i 和指针 j 指示文本串 T 和模式串 p 中当前正在对比的字符。当发现文本串 T 的某个字符与模式串 p 不匹配的时候,j 回退到开始位置,i 回退到之前匹配开始位置的下一个位置上(下图的B),继续匹配,直到能够与匹配串对上位置(下图第二个A),如下图所示。
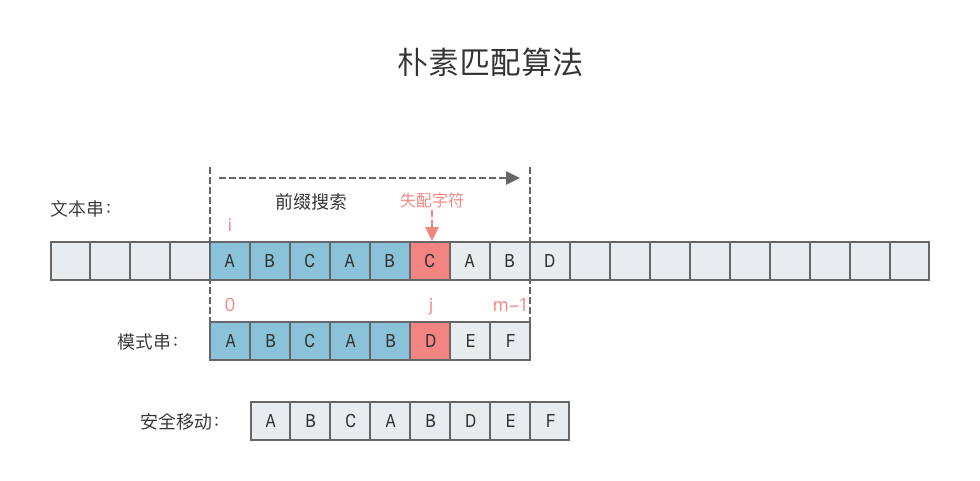
那么有没有哪种算法,可以让 i 不发生回退,一直向右移动呢?
2.2.1 改进算法:KMP
如果我们可以通过每一次的失配而得到一些「信息」,并且这些「信息」可以帮助我们跳过那些不可能匹配成功的位置,那么我们就能大大减少模式串与文本串的匹配次数,从而达到快速匹配的目的。
- 每一次失配所告诉我们的信息是:主串的某一个子串等于模式串的某一个前缀。
比如文本串
T[i: i + m]与模式串p的失配是下标位置j上发生的,那么文本串T从下标位置i开始连续的j - 1个字符,一定与模式串p的前j - 1个字符一模一样,即:T[i: i + j] == p[0: j]。例如上图中,失配是在下标
i+5这个位置发生的,那么失配位置的前5个字符,一定与模式串p的前5个字符一模一样,即:"ABCAB" == "ABCAB"。
- 模式串的前
5个字符中,前2位前缀和后2位后缀又是相同的,即"AB" == "AB"。
所以根据上面的信息,我们可以推出:文本串子串的后 2 位后缀和模式串子串的前 2 位是相同的,即 T[i + 3: i + 5] == p[0: 2],而这部分(即下图中的蓝色部分)是之前已经比较过的,不需要再比较了,可以直接跳过。
那么我们就可以将文本串中的 T[i + 5] 对准模式串中的 p[2],继续进行对比。这样 i 就不再需要回退了,可以一直向右移动匹配下去。在这个过程中,我们只需要将模式串 j 进行回退操作即可。
实际上,我们会创建一个next数组作为「部分匹配表」,
next[j]表示的含义是:记录下标 j 之前(包括 j)的模式串p中,最长相等前后缀的长度。下一节会详细说明。
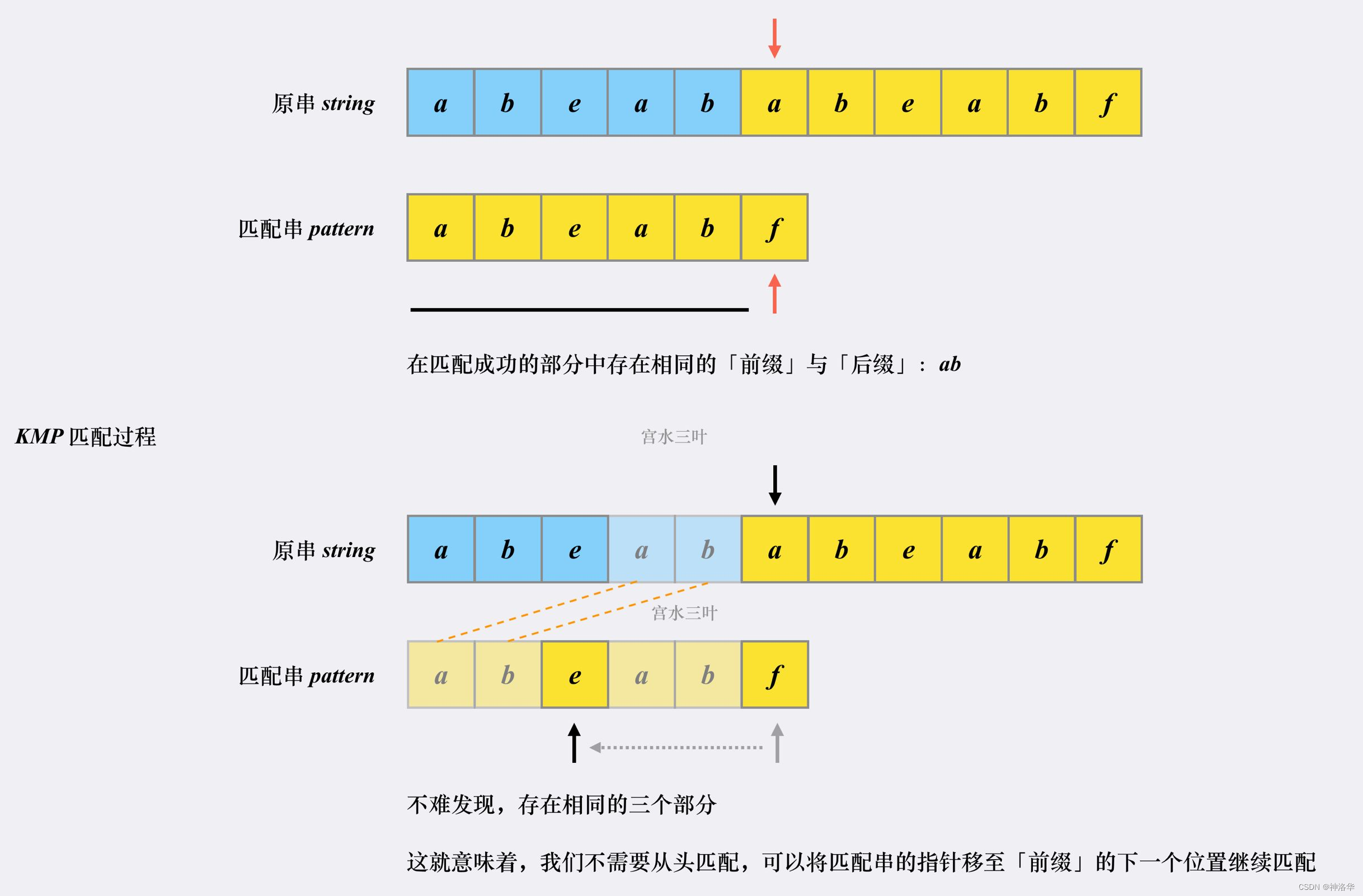
由于模式串数组中,next[4] == 2,所以不用回退i,而是将j移动到下标为2的位置,让T[i + 5]直接对准p[2],然后继续进行比对。也就是说,匹配失败时,匹配串会检查之前已经匹配成功的部分中里是否存在相同的「前缀」和「后缀」。如果存在,则跳转到「前缀」的下一个位置继续往下匹配:
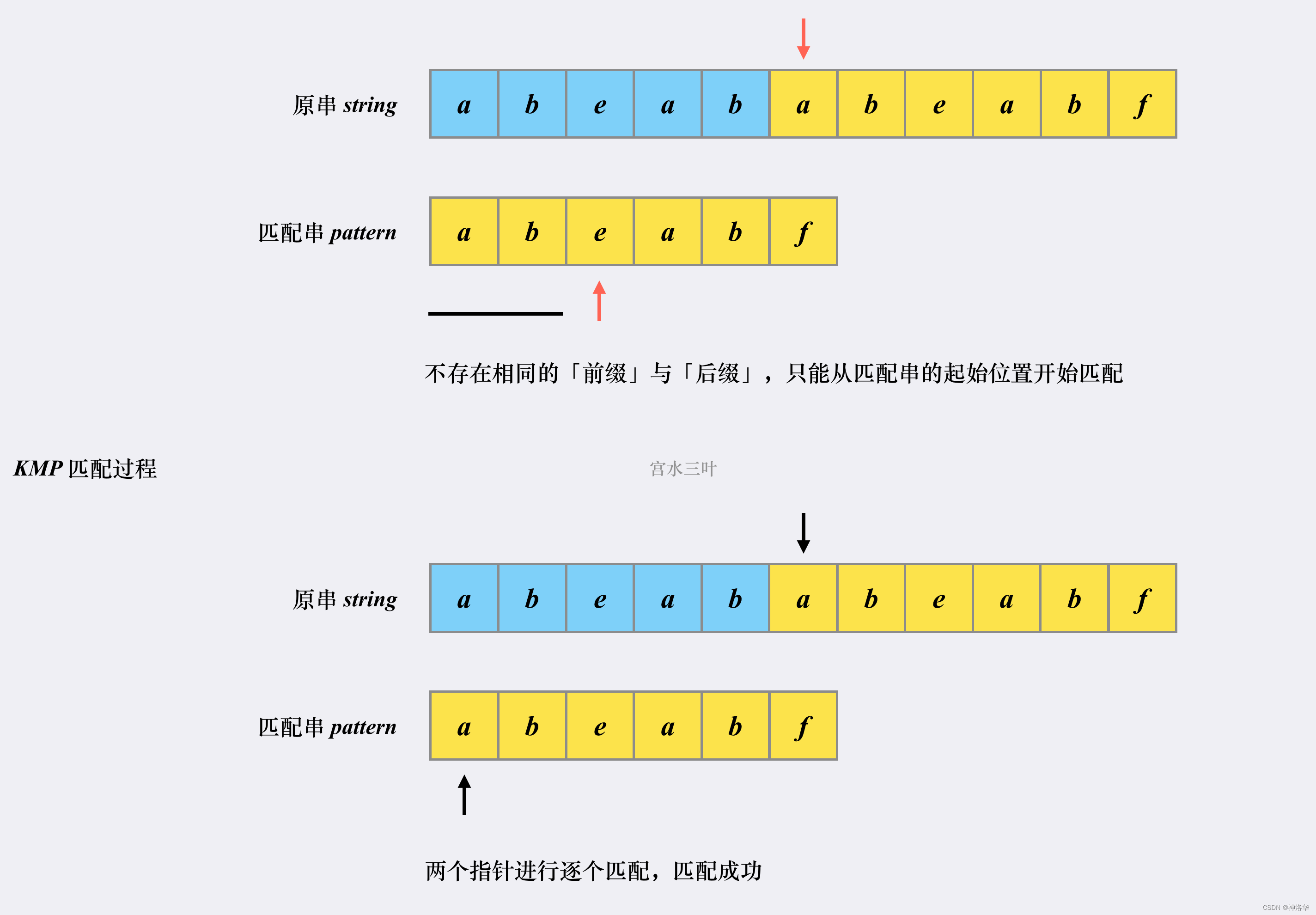
跳转到下一匹配位置后,尝试匹配,发现两个指针的字符对不上,并且此时匹配串指针前面不存在相同的「前缀」和「后缀」,这时候只能回到匹配串的起始位置重新开始:
KMP 算法就是使用了这样的思路,对模式串 p 进行了预处理,计算出一个 「部分匹配表」(也叫PMT:Partial Match Table)**,用一个数组 next 来记录。然后在每次失配发生时,不回退文本串的指针 i,而是根据「部分匹配表」中模式串失配位置 j 的前一个位置的值,即 next[j - 1] 的值来决定模式串可以向右移动的位数。
上文提到的「部分匹配表PMT」,也叫做「前缀表」,在 KMP 算法中使用 next 数组存储。next[j] 表示的含义是:记录下标 j 之前(包括 j)的模式串 p 中,最长相等前后缀的长度。 也可以理解为,PMT中的值是 字符串的前缀集合与后缀集合的交集中最长元素的长度。</font >
- 前缀:
- 如果字符串A和B,存在
A=BS,其中S是任意的非空字符串,那就称B为A的前缀。- 例如,”
Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”},我们把所有前缀组成的集合,称为字符串的前缀集合。- 后缀:
- 若有
A=SB, 其中S是任意的非空字符串,那就称B为A的后缀- 例如,”
Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”},然后把所有后缀组成的集合,称为字符串的后缀集合。- 对于字符串”
ababa”,它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”},它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}, 两个集合的交集为{”a”, ”aba”},其中最长的元素为”aba”,长度为3。- 要注意的是,字符串本身并不是自己的前缀或者后缀。
举个例子来说明一下,以 p = "ABCABCD" 为例。
next[0] = 0,因为"A"中无有相同前缀后缀,最大长度为0。next[1] = 0,因为"AB"中无相同前缀后缀,最大长度为0。next[2] = 0,因为"ABC"中无相同前缀后缀,最大长度为0。next[3] = 1,因为"ABCA"中有相同的前缀后缀"a",最大长度为1。next[4] = 2,因为"ABCAB"中有相同的前缀后缀"AB",最大长度为2。next[5] = 3,因为"ABCABC"中有相同的前缀后缀"ABC",最大长度为3。next[6] = 0,因为"ABCABCD"中无相同前缀后缀,最大长度为0。
同理也可以计算出 "ABCABDEF" 的前缀表为 [0, 0, 0, 1, 2, 0, 0, 0]。"AABAAAB" 的前缀表为 [0, 1, 0, 1, 2, 2, 3]。"ABCDABD" 的前缀表为 [0, 0, 0, 0, 1, 2, 0]。
在之前的例子中,当 p[5] 和 T[i + 5] 匹配失败后,根据模式串失配位置 j 的前一个位置的值,即 next[4] = 2,我们直接让 T[i + 5] 直接对准了 p[2],然后继续进行比对,如下图所示。
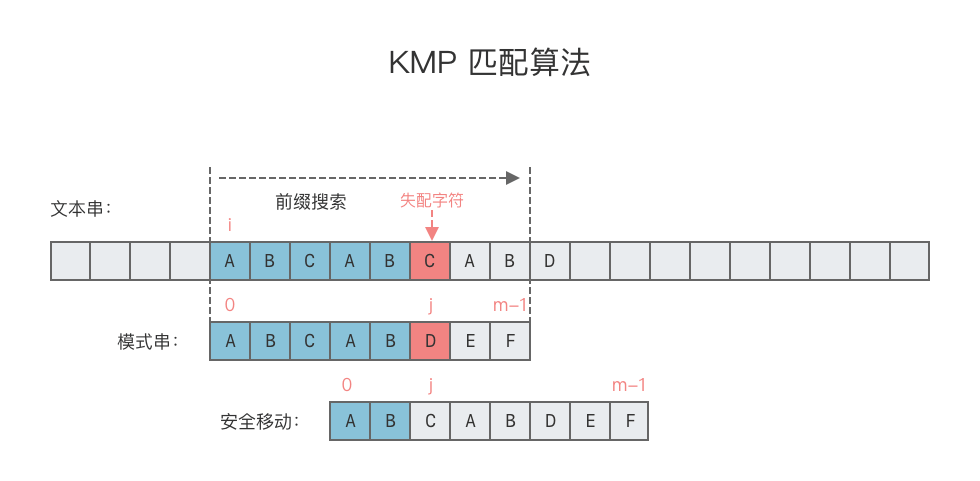
但是这样移动的原理是什么?
如果文本串 T[i: i + m] 与模式串 p 的失配是在第 j 个下标位置发生的,那么:
- 文本串
T从下标位置i开始连续的j个字符,一定与模式串p的前j个字符一模一样,即:T[i: i + j] == p[0: j](上图中的"ABCAB" == "ABCAB")。 而如果模式串
p的前j个字符中,前k位前缀和后k位后缀相同,("ABCAB"中有相同的前后缀"AB",即k=2)那么可以断言:文本串中i指针失配位置之前的k位(”AB“)一定与模式字符串的第0位至第k位是相同的(”AB“),即长度为k的后缀与前缀相同。这样一来,我们就可以将这些字符段的比较省略掉。具体的做法是,保持
i指针不动,然后将j指针指向模式字符串的next[j −1]位即可(表示模式串中,前j-1个子符里,最长相同前后缀的长度k)。
其实相当于因为模式串存在相同的前后缀,所以失配后,模式串不用退回起始位置,退到相同前缀的下一位置就行。
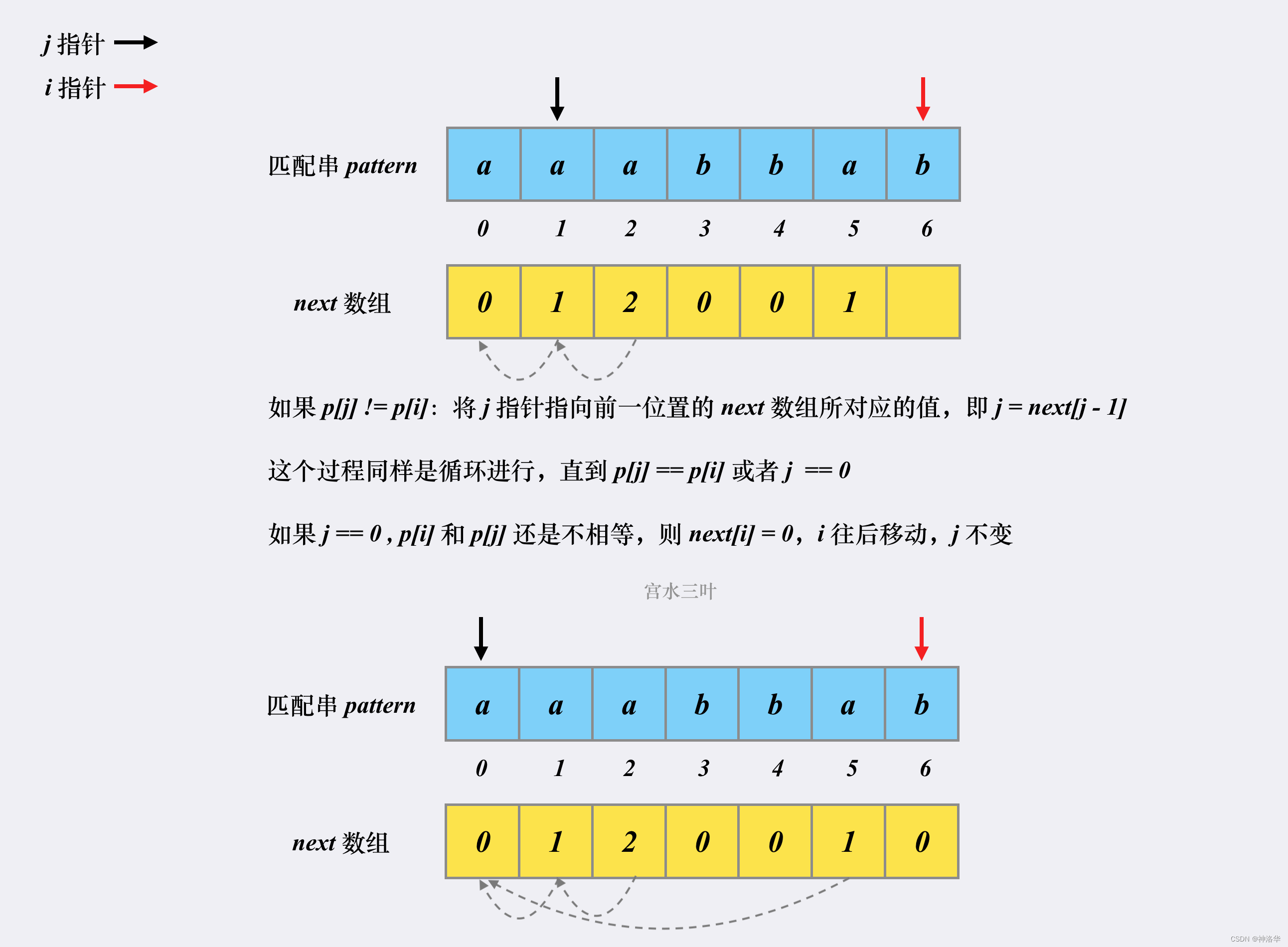
2.2.4 next 数组的构造
其实,求next数组的过程完全可以看成字符串匹配的过程,即以模式字符串为文本串串,以模式字符串的前缀为目标字符串,一旦字符串匹配成功,那么当前的next值就是匹配成功的字符串的长度。
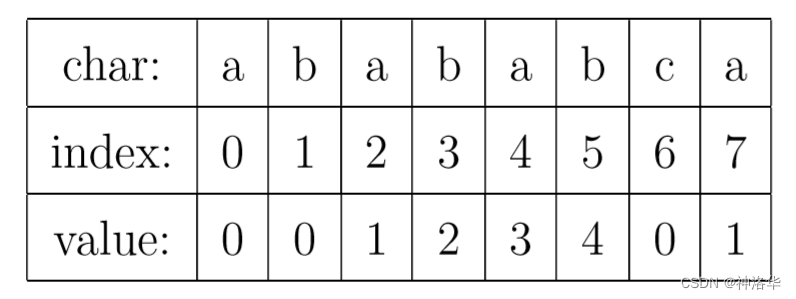
具体来说,就是从模式字符串的第一位(注意,不包括第0位)开始对自身进行匹配运算。 在任一位置,能匹配的最长长度就是当前位置的next值。如下图所示。
数组下标从0开始,所以图中应该是
next[5]=4,以此类推。下图模式串有next=[0, 0, 1, 2, 3, 4, 0, 1]
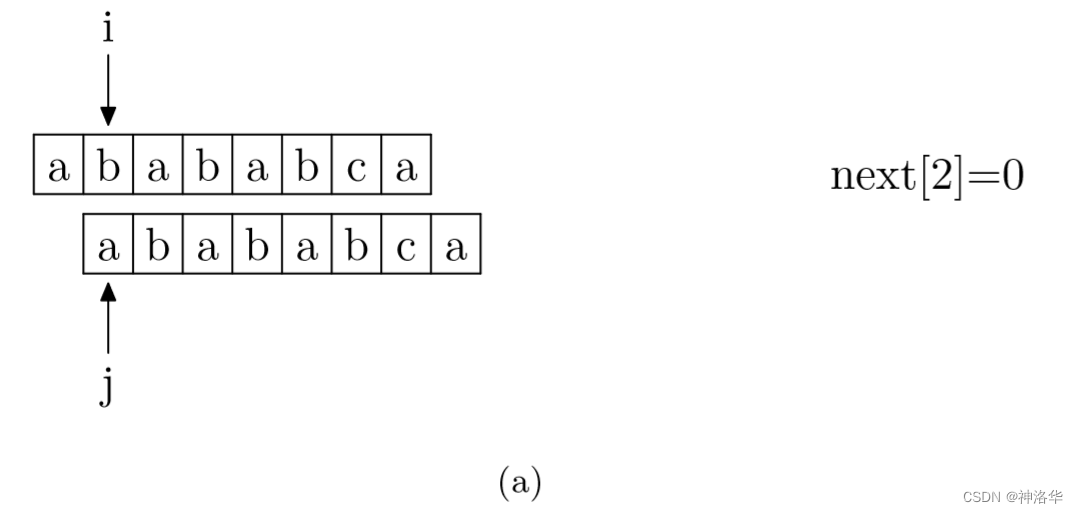
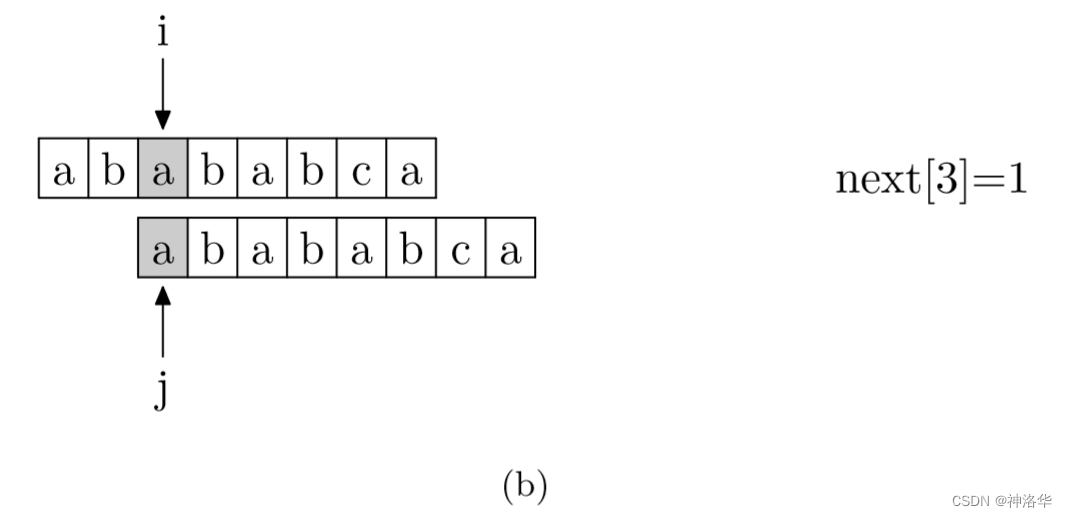
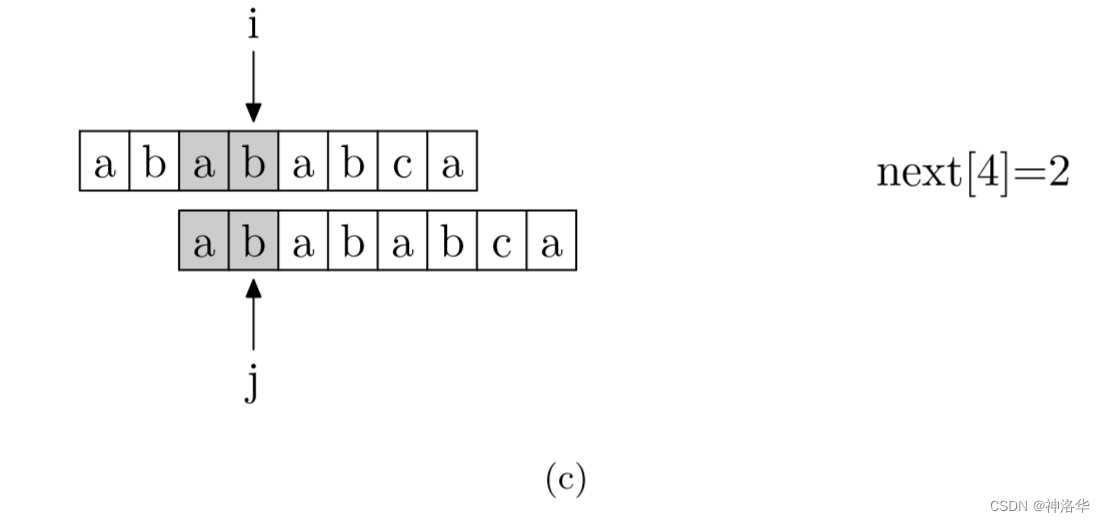
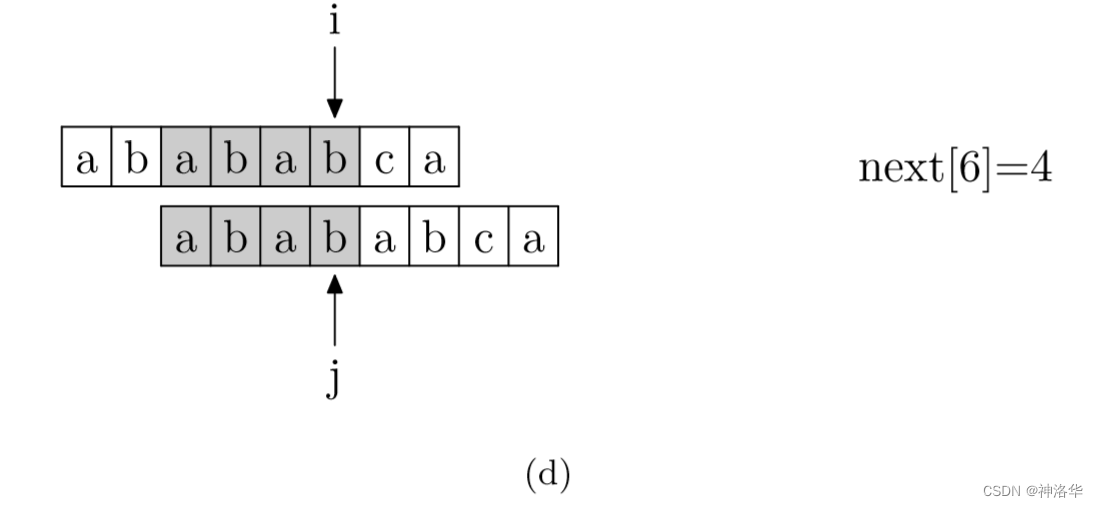
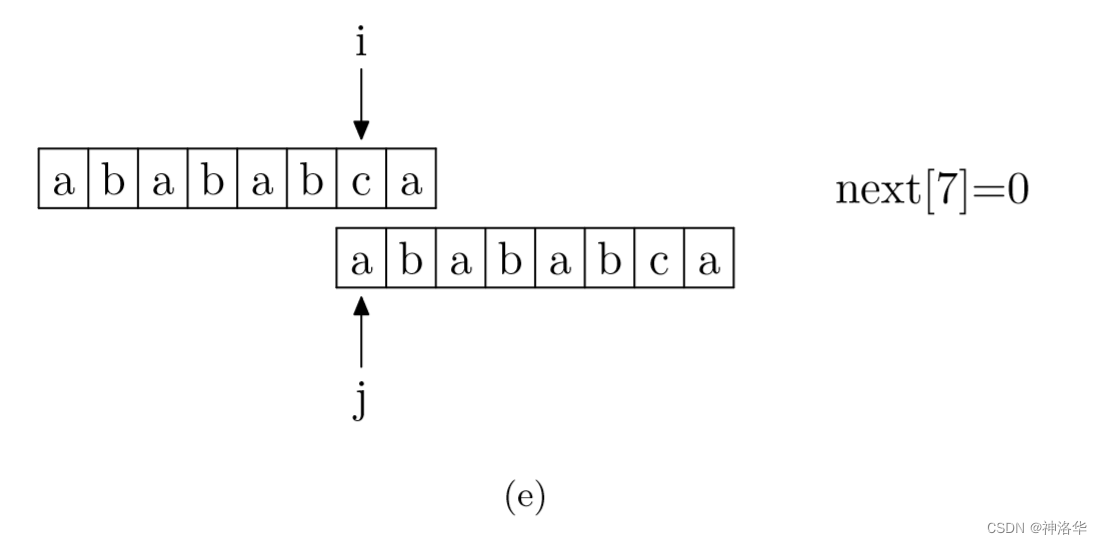
这样我们就可以使用KMP本身的匹配原理来计算next数组。
- 我们将模式串p本身即作为文本串也作为模式串,同样用指针
i和j来遍历。因为文本串第一个位置即使匹配上 ,也有next[0]=0,而不等于1,所以初始时令j = 0,i = 1。 - 遍历文本串和模式串:
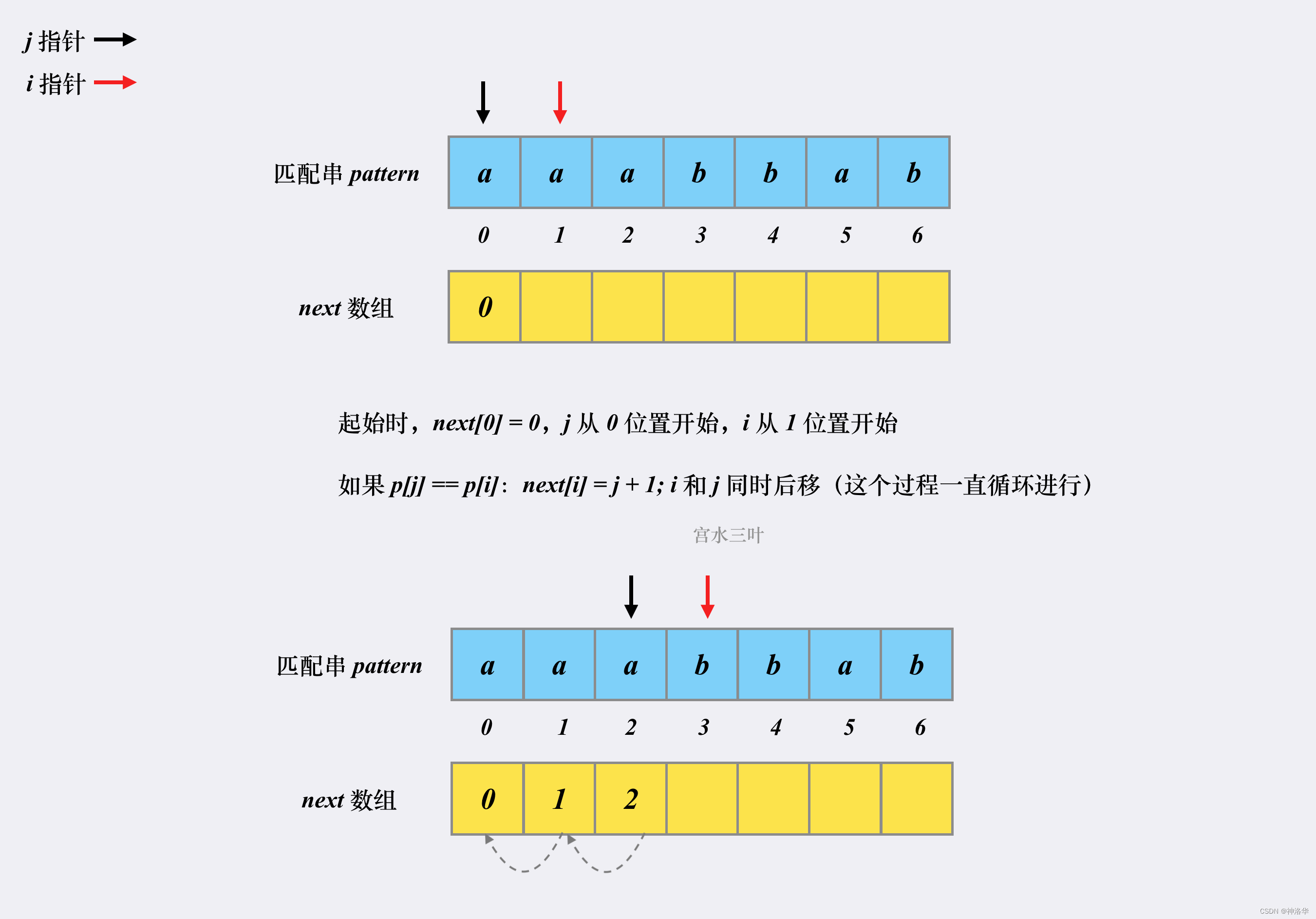
- 如果
p[i] != p[j],说明文本串在此位置失配,同上面所讲,i不动,模式串指针j不断回退到next[j - 1]位置。- 如果回退几次后,有
p[i] == p[j],说明匹配上了一个字符,令j右移,此时此时j既是前缀下一次进行比较的下标位置,又是当前最长前后缀的长度,所以next[i]=j。最后移动指针i遍历下一个位置; - 如果一直回退到
j=0,表示文本串在i位置匹配不到任何一个字符,next[i]=0=j,i+=1;
- 如果回退几次后,有
- 如果
p[i] == p[j],同样先将j += 1,next[i]=j,i+=1;
- 如果
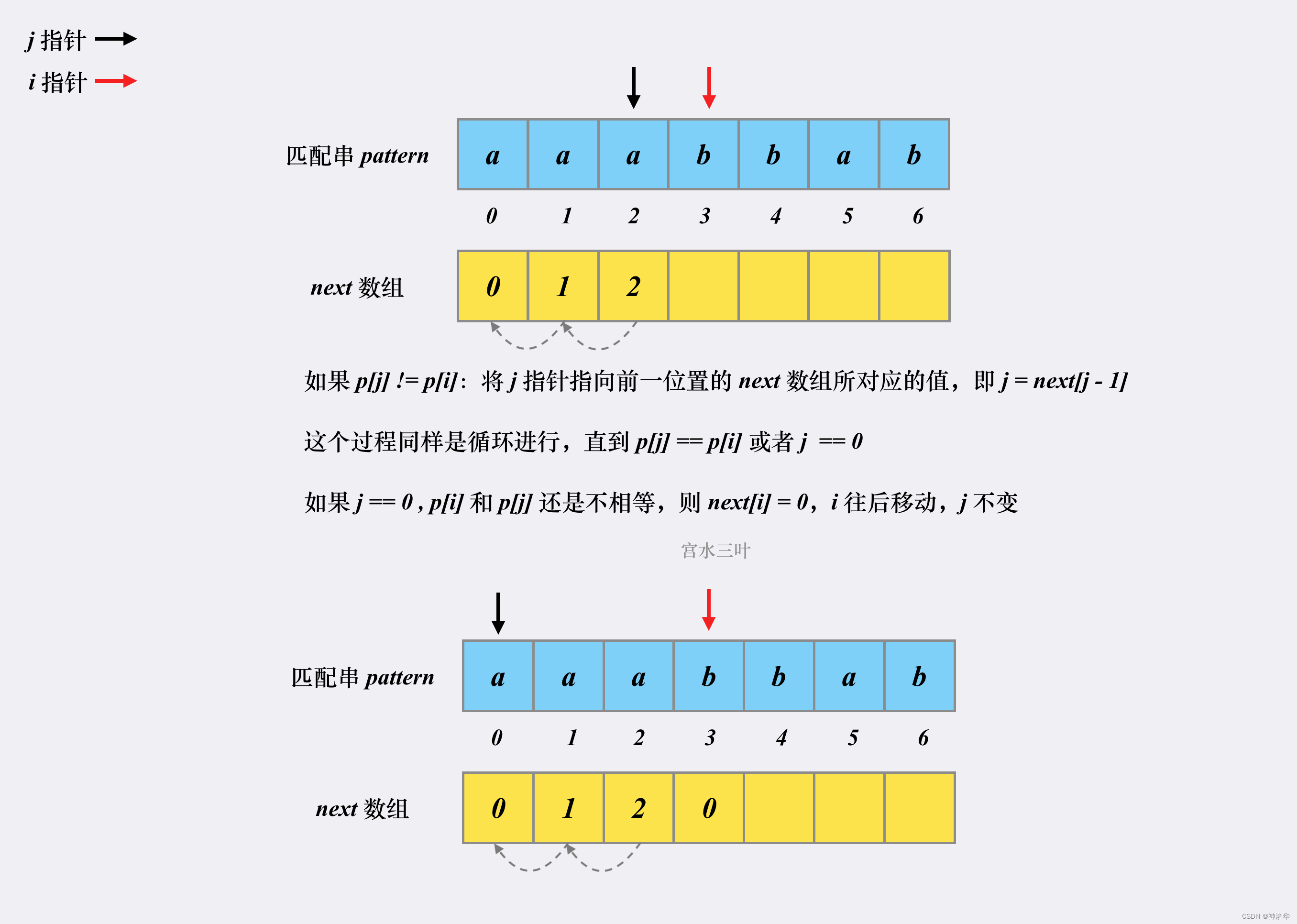
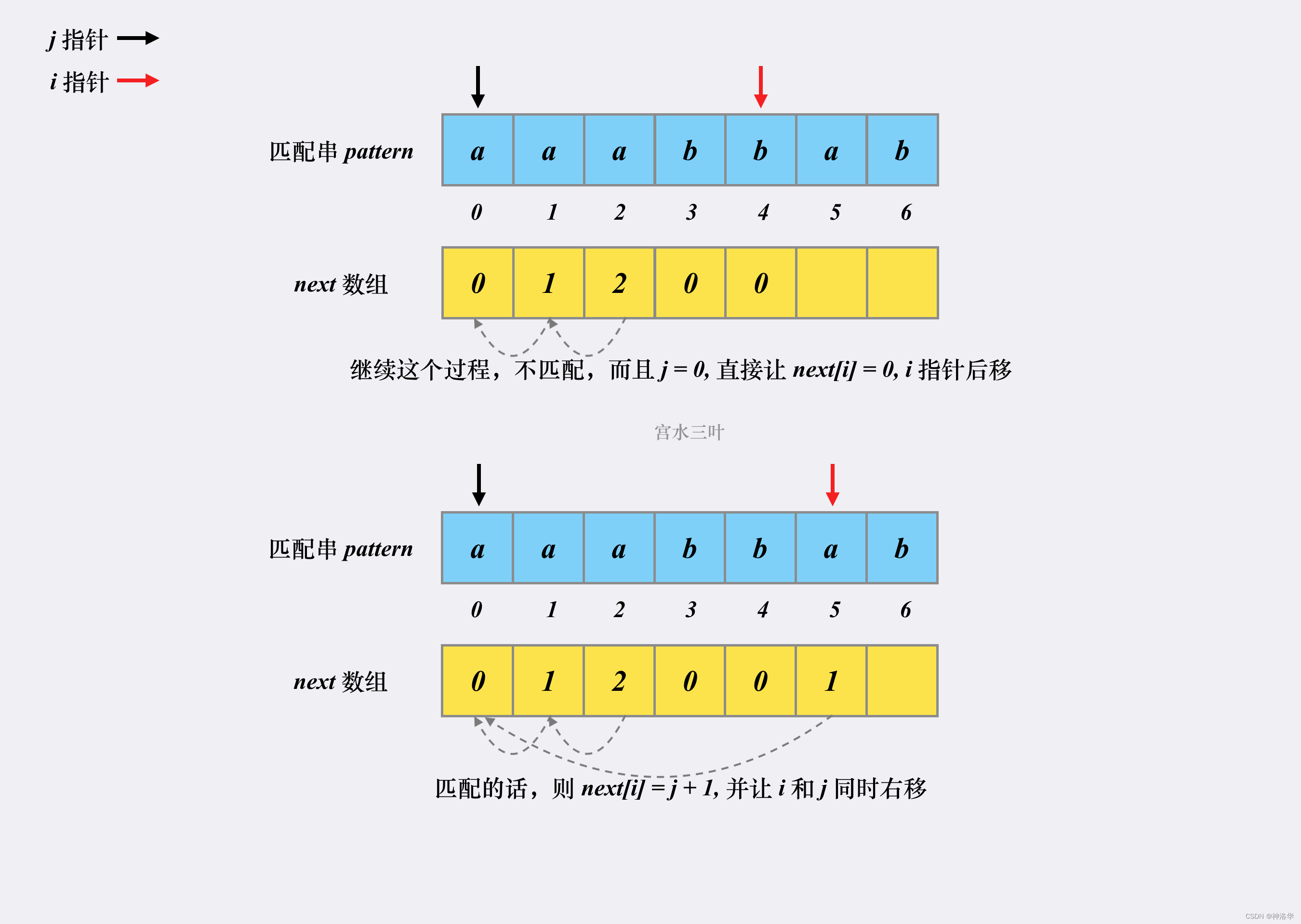
- 如果
p[j]==p[i],j先后移,next[i]=j,然后i后移;- 如果不匹配,前缀指针回退,退到前一位置的
next值,即j=next[j-1],不停回退,直到p[j]==p[i],或者j=0表示退到模式串开头位置,此时next[i]=0(因为j=0,所以依旧有next[i]=j),表示没有匹配的共同前后缀。
2.2.5 KMP 算法整体步骤和代码实现
- 根据
next数组的构造步骤生成「前缀表」next。 - 使用两个指针
i、j,其中i指向文本串中当前匹配的位置,j指向模式串中当前匹配的位置。初始时,i = 0,j = 0。 - 循环判断模式串前缀是否匹配成功,如果模式串前缀匹配不成功,将模式串进行回退,即
j = next[j - 1],直到j == 0时或前缀匹配成功时停止回退。 - 如果当前模式串前缀匹配成功,则令模式串向右移动
1位,即j += 1。 - 如果当前模式串 完全 匹配成功,则返回模式串
p在文本串T中的开始位置,即i - j + 1。 - 如果还未完全匹配成功,则令文本串向右移动
1位,即i += 1,然后继续匹配。 - 如果直到文本串遍历完也未完全匹配成功,则说明匹配失败,返回
-1。
# 生成 next 数组 |
2.2.5 KMP 算法分析
- KMP 算法在构造前缀表阶段的时间复杂度为 $O(m)$,其中 $m$ 是模式串
p的长度。 - KMP 算法在匹配阶段,是根据前缀表不断调整匹配的位置,文本串的下标
i并没有进行回退,可以看出匹配阶段的时间复杂度是 $O(n)$,其中 $n$ 是文本串T的长度。 - 所以 KMP 整个算法的时间复杂度是 $O(n + m)$,相对于朴素匹配算法的 $O(n * m)$ 的时间复杂度,KMP 算法的效率有了很大的提升。
参考资料
三、单模式串匹配练习
3.1 单模式串匹配题目
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 0028 | 找出字符串中第一个匹配项的下标 | Python | 字符串、双指针 | 简单 |
| 0459 | 重复的子字符串 | Python | 字符串、字符串匹配 | 简单 |
| 0686 | 重复叠加字符串匹配 | Python | 字符串、字符串匹配 | 中等 |
| 1668 | 最大重复子字符串 | |||
| 0796 | 旋转字符串 | Python | 字符串、字符串匹配 | 简单 |
| 1408 | 数组中的字符串匹配 | Python | 字符串、字符串匹配 | 简单 |
| 2156 | 查找给定哈希值的子串 | Python | 字符串、滑动窗口、哈希函数、滚动哈希 | 中等 |
3.2 找出字符串中第一个匹配项的下标
class Solution(object): |
3.3 重复的子字符串
给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。输入: s = "abcabcabcabc"
输出: true
解释: 可由子串 "abc" 重复四次构成。 (或子串 "abcabc" 重复两次构成。)
- 思路一:官方题解

class Solution: |
思路二:KMP(参考《算法通关手册》)
我们知道 next[j] 表示的含义是:记录下标 j 之前(包括 j)的模式串 p 中,最长相等前后缀的长度。
而如果整个模式串 p 的最长相等前后缀长度不为 0,即 next[len(p) - 1] != 0 ,则说明整个模式串 p 中有最长相同的前后缀。假设 next[len(p) - 1] == k,则说明 p[0: k] == p[m - k: m]。比如字符串 “abcabcabc”,最长相同前后缀为 “abcabc” = “abcabc”。
- 如果最长相等的前后缀是重叠的,比如之前的例子 “abcabcabc”。
- 如果我们去除字符串中相同的前后缀的重叠部分,剩下两头前后缀部分(这两部分是相同的)。然后再去除剩余的后缀部分,只保留剩余的前缀部分。比如字符串 “abcabcabc” 去除重叠部分和剩余的后缀部分之后就是 “abc”。实际上这个部分就是字符串去除整个后缀部分的剩余部分。
- 如果整个字符串可以通过子串重复构成的话,那么这部分就是最小周期的子串。
- 我们只需要判断整个子串的长度是否是剩余部分长度的整数倍即可。也就是判断
len(p) % (len(p) - next[size - 1]) == 0是否成立,如果成立,则字符串 s 可由s[0: len(p) - next[size - 1]]构成的子串重复构成,返回True。否则返回False。
- 如果最长相等的前后缀是不重叠的,那我们可将重叠部分视为长度为
0的空串,则剩余的部分其实就是去除后缀部分的剩余部分,上述结论依旧成立。class Solution:
def repeatedSubstringPattern(self, s: str) -> bool:
# 创建next数组
le=len(s)
if le==1:
return False
j=0
next=[0 for _ in range(le)]
for i in range(1,le):
while j>0 and s[i]!=s[j]:
j=next[j-1]
if s[i]==s[j]:
j+=1
next[i]=j
# next数组最后一位的值,表示模式串的最长相等前后缀长度。
# 将其除去前后缀重叠部分和剩余的后缀部分,就是剩余前缀部分。
# 这部分就是最小周期长度,可以被模式串长度整除
if next[le-1]!=0 and le%(le-next[le-1])==0:
return True
return False3.4 重复叠加字符串匹配
给定两个字符串 a 和 b,寻找重复叠加字符串 a 的最小次数,使得字符串 b 成为叠加后的字符串 a 的子串,如果不存在则返回 -1。
输入:a = "abcd", b = "cdabcdab" |
首先,可以分析复制次数的「下界」和「上界」为何值:
- 「下界」:至少将 a 复制长度大于等于 b 的长度,才有可能匹配
- 「上界」:由于主串是由 a 复制多次而来,并且是从主串中找到子串 b,因此可以明确子串的起始位置,不会超过 a 的长度。即长度越过 a 长度的起始匹配位置,必然在此前已经被匹配过了。由此,我们可知复制次数「上界」最多为「下界 + 1」

class Solution: |
如果用KMP算法代替find函数写,就是:
class Solution: |
3.5 最大重复子字符串
给你一个字符串 sequence ,如果字符串 word 连续重复 k 次形成的字符串是 sequence 的一个子字符串,那么单词 word 的 重复值为 k 。单词 word 的 最大重复值 是单词 word 在 sequence 中最大的重复值。如果 word 不是 sequence 的子串,那么重复值 k 为 0 。
给你一个字符串 sequence 和 word ,请你返回 最大重复值 k 。
输入:sequence = "ababc", word = "ba" |
class Solution(object): |
class Solution(object): |
3.6 旋转字符串
- 给定两个字符串, s 和 goal。如果在若干次旋转操作之后,s 能变成 goal ,那么返回 true 。
- s 的 旋转操作 就是将 s 最左边的字符移动到最右边。
输入: s = "abcde", goal = "cdeab" |
class Solution(object): |