@[toc]
一、 树
1.1 树的定义
树(Tree):由 $n \ge 0$ 个节点与节点之间的边组成的有限集合。当 $n = 0$ 时称为空树,当 $n > 0$ 时称为非空树。
树由若干节点,以及两两连接节点的边组成,并具有以下性质:
- 其中一个节点被设定为根;
- 每个节点n(除根节点),都恰连接一条来自节点p的边,p是n的父节点;
- 每个节点从根开始的路径是唯一的。
- 如果每个节点最多有两个子节点,这样的树称为“二叉树”
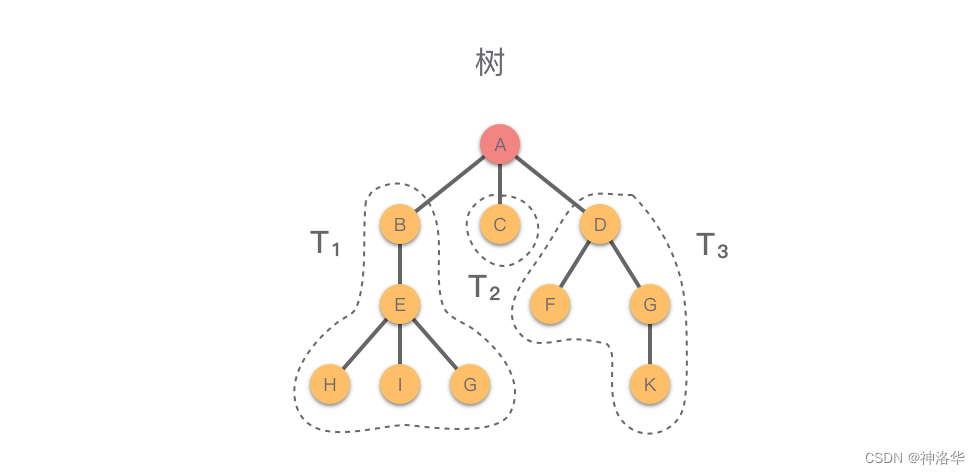
之所以把这种数据结构称为「树」是因为这种数据结构看起来就像是一棵倒挂的树,也就是说数据结构中的「树」是根朝上,而叶朝下的。如下图所示。
- 节点
Node:组成树的基本部分,每个节点具有名称,或“键值”,节点还可以保存额外数据项,数据项根据不同的应用而变。- 子节点
Children:入边均来自于同一个节点的若干节点,称为这个节点的子节点。 - 父节点
Parent:一个节点是其所有出边所连接节点的父节点。 - 兄弟节点
Sibling:具有同一个父节点的节点之间称为兄弟节点。 - 叶节点
Leaf:没有子节点的节点称为叶节点。 - 节点的度
Height:一个节点所含有的子树个数
- 子节点
根
Root:树中唯一一个没有入边的节点。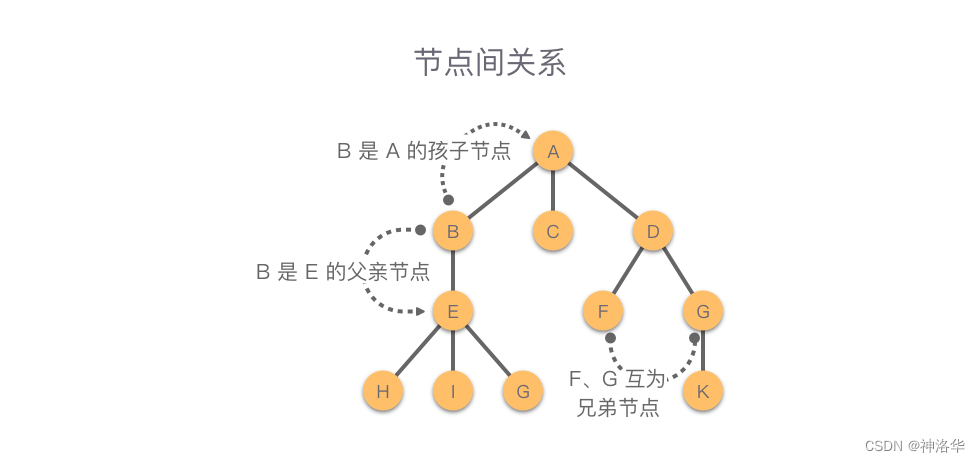
边
Edge:边是组成树的另一个基本部分。每条边恰好连接两个节点,表示节点之间具有关联,边具有出入方向;每个节点(除根节点)恰有一条来自另一节点的入边;每个节点可以有多条连到其他节点的出边。路径
Path:由边依次连接在一起的节点的有序列表,例如图中E到G的路径为E - B - A - D - G。- 路径长度:两个节点之间路径上经过的边数。例如图中
E到G的路径长度为 $4$。 - 子树
Subtree:一个节点和其所有子孙节点,以及相关边的集合。
如上图所示,红色节点 $A$ 是根节点,除了根节点之外,还有3棵互不相交的子树 $T_1(B、E、H、I、G)$、$T_2(C)$、$T_3(D、F、G、K)$。 - 层级
Level:从根节点开始到达一个节点的路径,所包含的边的数量,称为这个节点的层级。根节点层级为0。 - 高度
height:树中所有节点的最大层级称为树的高度。
除了上面树的集合定义(树是由节点和边组成的集合),还有一种递归的定义,树是:
- 空集
- 或者由根节点和0或多个子树构成。每个子树的根节点都跟树的根节点有边相连
1.2 二叉树
树根据节点的子树是否可以互换位置,可以分为有序树和无序树,二叉树是有序树的一种。
- 有序树:节点的各个⼦树从左⾄右有序, 不能互换位置。
- 二叉树(Binary Tree):树中各个节点的度不大于
2个的有序树,称为二叉树。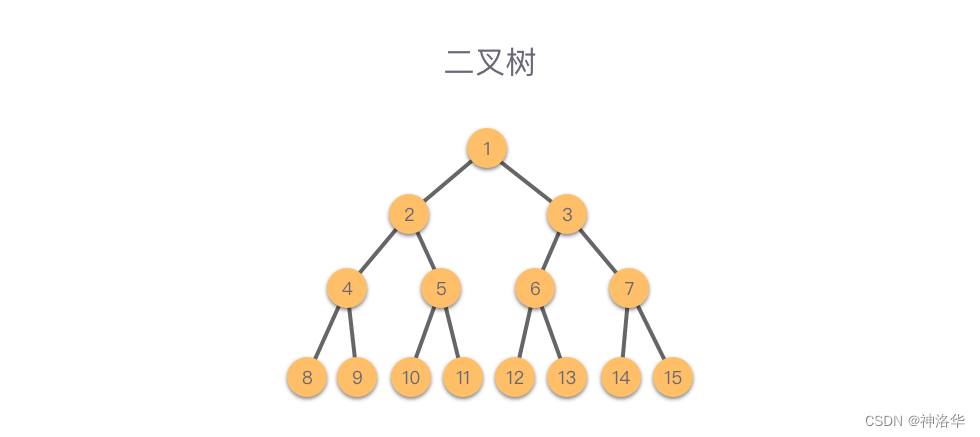
- 二叉树(Binary Tree):树中各个节点的度不大于
- 无序树:节点的各个⼦树可互换位置。
二叉树是种特殊的树(可以是空树),它最多有两个⼦树,分别为左⼦树和右⼦树,并且两个子树是有序的,不可以互换。也就是说,在⼆叉树中不存在度⼤于 $2$ 的节点。
二叉树在逻辑上可以分为 5种基本形态,如下图所示: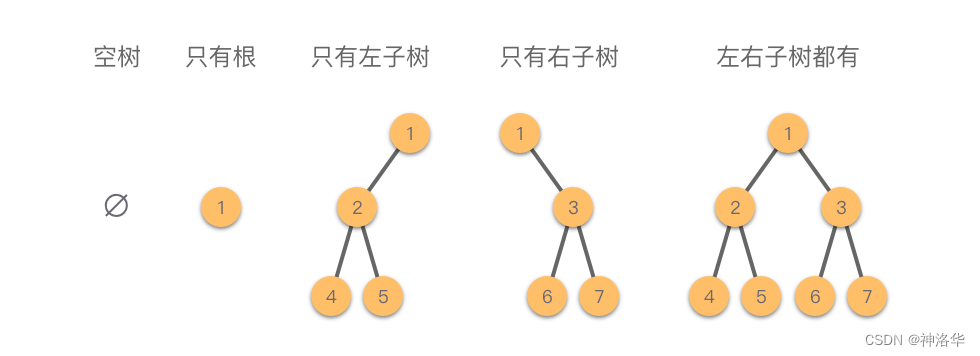
下面我们来介绍一些特殊的二叉树。
1.2.1 完全二叉树
完全二叉树(Complete Binary Tree):如果叶子节点只能出现在最下面两层,并且最下层的叶子节点都依次排列在该层最左边的位置上,具有这种特点的二叉树称为完全二叉树。
完全二叉树满足以下特点:
- 叶子节点只能出现在最下面两层。
- 每个内部节点都有两个子节点,最多只有一个内部节点例外。
- 最下层的叶子节点连续集中在最左边的位置上,即不存在只有右子树的情况。倒数第二层如果有叶子节点,则该层的叶子节点一定集中在右边的位置上。
- 同等节点数的二叉树中,完全二叉树的深度最小。
下面来看几个例子:

优先队列为了保持入队和出队复杂度都是$O(logn)$,所以采用完全二叉树来实现,下文优先队列会讲到。
为了使堆操作能保持在对数水平上,就必须采用二叉树结构。同时如果要使操作始终保持在对数数量级上,就必须始终保持二叉树的平衡,树根左右子树拥有相同数量的节点,所以考虑采用完全二叉树的结构来近似实现平衡。
1.2.1 满二叉树
满二叉树(Full Binary Tree):如果所有分支节点都存在左子树和右子树,并且所有叶子节点都在同一层上,则称该二叉树为满二叉树。
满二叉树满足以下特点:
- 叶子节点只出现在最下面一层。
- 非叶子节点的度一定为 $2$。
- 在同等深度的二叉树中,满二叉树的节点个数最多,叶子节点个数最多。
如果我们对满二叉树的节点进行编号,根结点编号为 $1$,然后按照层次依次向下,每一层从左至右的顺序进行编号。则深度为 $k$ 的满二叉树最后一个节点的编号为 $2^k - 1$。

1.2.3 二叉堆
堆(Heap):符合以下两个条件之一的完全二叉树:
- 大顶堆:根节点值 ≥ 子节点值。
- 小顶堆:根节点值 ≤ 子节点值。
完全二叉树中,只规定了元素插入的方式,没有按照元素值的大小规定其在树中的顺序。二叉堆是按照一定的堆次序
Heap Order排列的完全二叉树,分为两种:
- 最小堆
min heap(小顶堆):任何一个父节点的key都要小于其所有子节点的key,如下图二;- 最大堆
max heap(大顶堆):任何一个父节点的key都要大于其所有子节点的key,如下图一。
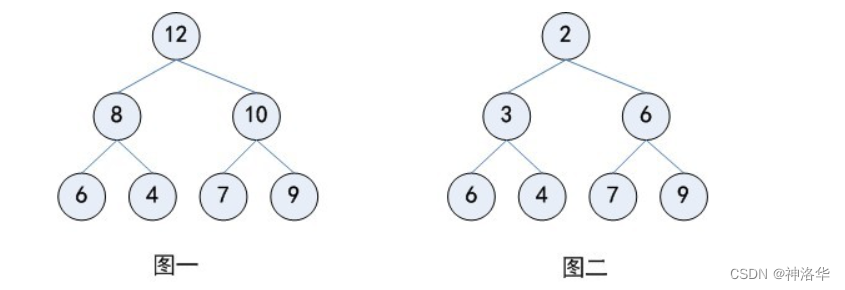
二叉堆中,任何一条路径,均是一个已排序数列,所以是部分有序。
1.2.4 二叉搜索树
二叉搜索树(Binary Search Tree):也叫做二叉查找树。二叉搜索树中,所有左子树上的节点都小于其根节点的值,所有右子树上的节点的值都大于其根节点的值,即恒有root.left.val<root.val<root.right.val。如下图所示,这 $3$ 棵树都是二叉搜索树。

平衡二叉搜索树(Balanced Binary Tree):一种结构平衡的二叉搜索树。即叶节点高度差的绝对值不超过 $1$,并且左右两个子树都是一棵平衡二叉搜索树。平衡二叉树可以在 $O(logn)$ 内完成插入、查找和删除操作。最早被发明的平衡二叉搜索树为 「AVL 树(Adelson-Velsky and Landis Tree))」。
AVL 树满足以下性质:
- 空二叉树是一棵 AVL 树。
- 如果 T 是一棵 AVL 树,那么其左右子树也是 AVL 树,并且 $|h(ls) - h(rs)| \le 1$,$h(ls)$ 是左子树的高度,$h(rs)$ 是右子树的高度。
- AVL 树的高度为 $O(log n)$。
如图所示,前 $2$ 棵树是平衡二叉搜索树,最后一棵树不是平衡二叉搜索树,因为这棵树的左右子树的高度差的绝对值超过了 $1$。
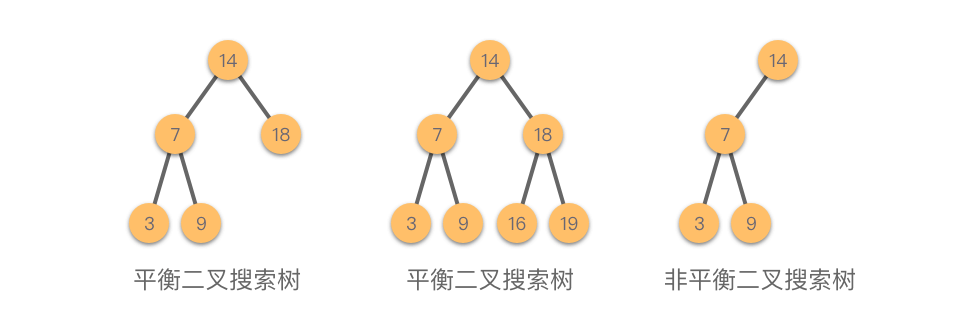
1.3 二叉树的实现
1.3.1 嵌套列表法(顺序存储)
可以使用Python List来实现二叉树数据结构。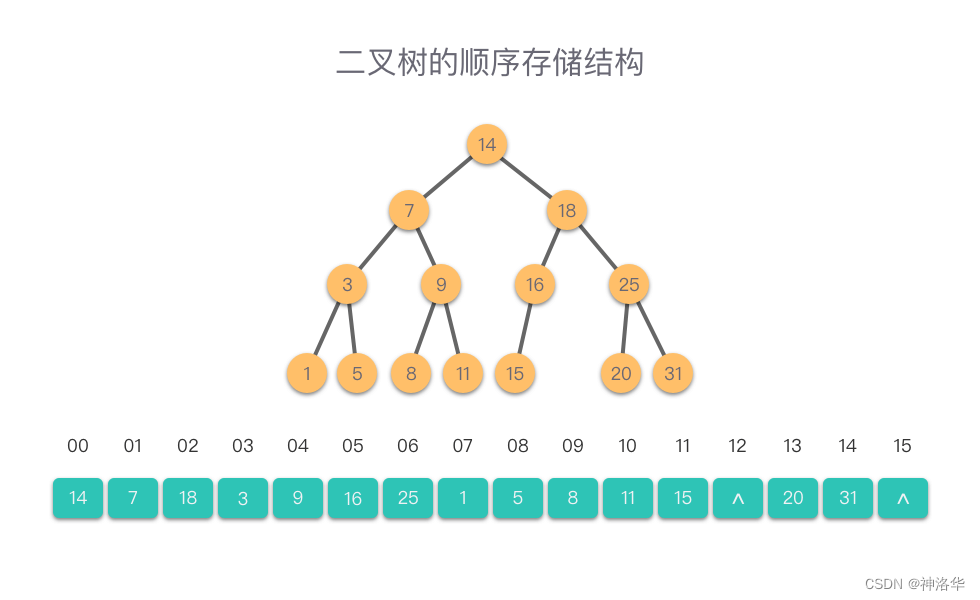
- 递归的嵌套列表实现二叉树,由具有3个元素的列表实现:
[root, left, right],这里left和right指的是左子树和右子树,所以是一个递归的表示。- 第1个元素为根节点的值;
- 第2个元素是左子树(所以也是一个列表);
- 第3个元素是右子树(所以也是一个列表);
- 叶节点没有子节点,其子树是一个空列表
- 对于二叉树,根是
myTree[0],左子树myTree[1],右子树myTree[2]。 嵌套列表法的优点:子树的结构与树相同,是一种递归数据结构;很容易扩展到多叉树,仅需要增加列表元素即可。

嵌套列表法代码:
def BinaryTree(r): # 创建仅有根节点的二叉树 |
代码运行示例:


对于完全二叉树(尤其是满二叉树)来说,采用顺序存储结构比较合适,它能充分利用存储空间;而对于一般二叉树,如果需要设置很多的「空节点」,则采用顺序存储结构就会浪费很多存储空间。
由于顺序存储结构固有的一些缺陷,会使得二叉树的插入、删除等操作不方便,效率也比较低。对于二叉树来说,当树的形态和大小经常发生动态变化时,更适合采用链式存储结构。
1.3.2 节点链接法(链式存储)
二叉树采用链式存储结构时,每个链节点包含一个用于数据域 val,存储节点信息;还包含两个指针域 left 和 right,分别指向左右两个子节点。当左子节点或者右子节点不存在时,相应指针域值为空。二叉链节点结构如下图所示。

定义BinaryTree类
- 每个节点的val保存其节点的数据项(数值)
成员
left/right children保存指向左右子树的引用(同样是BinaryTree对象)。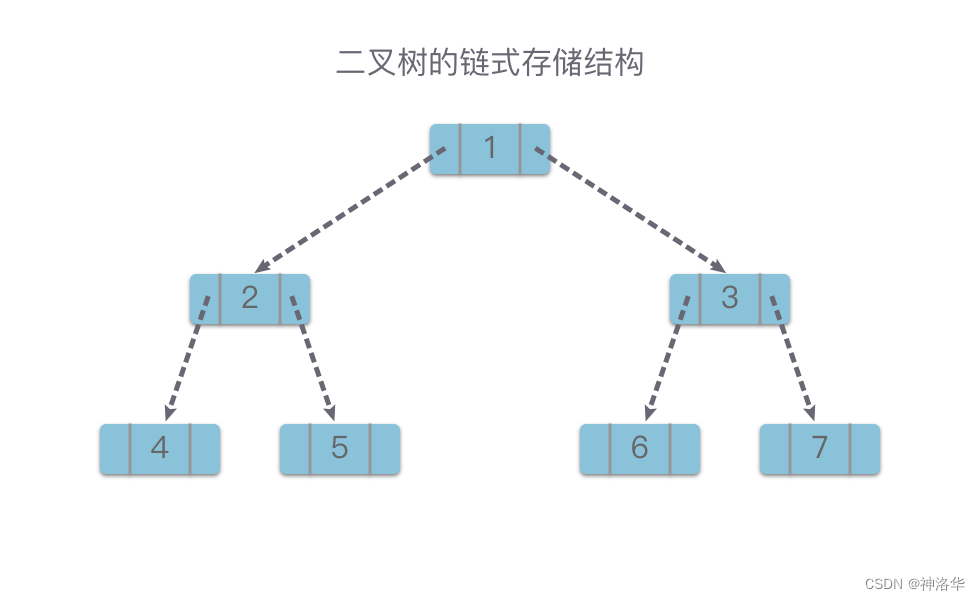
节点链接法代码:
class BinaryTree: |
代码运行示例:
二叉树的链表存储结构具有灵活、方便的特点。节点的最大数目只受系统最大可存储空间的限制。一般情况下,二叉树的链表存储结构比顺序存储结构更省空间(用于存储指针域的空间开销只是二叉树中节点数的线性函数),而且对于二叉树实施相关操作也很方便,因此,一般我们使用链式存储结构来存储二叉树。
1.4 树的应用:表达式解析
- 可以将表达式表示为树结构,叶节点保存操作数,内部节点保存操作符。
- 表达式层次决定计算的优先级,越底层的表达式,优先级越高。例如全括号表达式:
((7+3)*(5-2)) - 树中的每个子树都表示一个子表达式。将子树替换为子表达式值的节点,即可实现求值。


- 从全括号表达式创建表达式解析树
扫描:
首先,全括号表达式要分解为Token列表。其单词分为括号、操作符和操作数这几类,左括号是表达式的开始,而右括号是表达式的结束。下面是一个实例演示,全括号表达式为(3+(4*5)),灰色表示当前节点: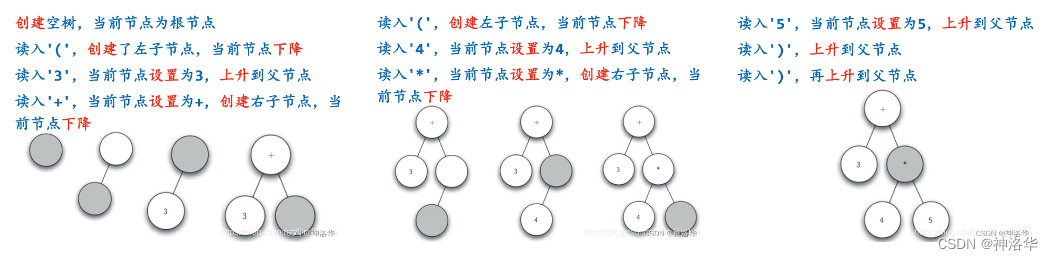
归纳定义表达式解析树规则
从左到右扫描全括号表达式的每个单词,依据规则建立解析树。- 当前单词是
"(":为当前节点添加一个新节点作为其左子节点insertLeft,当前节点下降为这个新节点getLeftChild; - 当前单词是操作符
“+, -, *, /”:将当前节点的值设为此符号setRootVal,为当前节点添加一个新节点作为其右子节点insertRight,当前节点下降为这个新节点getRightChild; - 当前单词是操作数:将当前节点的值设为此数,当前节点上升到父节点;
- 当前单词是
")":则当前节点上升到父节点。
- 当前单词是
- 创建树的过程中,关键的是对当前节点的跟踪。
从上面步骤可以看到,上升到父节点目前没有支持的方法。我们可以用一个栈来记录跟踪父节点。当前节点下降时,将下降前的节点push入栈;当前节点需要上升至父节点时,上升到pop出栈的节点即可。
表达式解析树创建代码:
def buildParseTree(s): |
- 利用表达式解析树求值
由于二叉树BinaryTree是一个递归数据结构,自然可以用递归算法来处理。求值递归函数evaluate,可从树的底层子树开始,逐步向上层求值,最终得到整个表达式的值。
- 求值递归函数evaluate的递归三要素:
- 基本结束条件:叶节点是最简单的子树,没有左右子节点,其根节点的数据项即为子表达式树的值。
- 缩小规模:将表达式树分为左子树、右子树,即为缩小规模。
- 调用自身:分别调用evaluate计算左子树和右子树的值,然后将左右子树的值依根节点的操作符进行计算,从而得到表达式的值。
- 一个增加程序可读性的技巧:引用函数
operator。
如果使用if-else语句,判断操作符,来进行计算,随着表达式增多,可读性会变差。这里调用python内置函数operator,其包含了所有的操作符。我们将op设为+-*/这些不同的操作符,就可以使用相同的语句op(1,2)来实现不同的计算,增加代码的可读性。
import operator |
表达式解析树求值代码实现:
import operator |
二、 树的遍历Tree Traversals
树的遍历:指的是从根节点出发,按照某种次序依次访问二叉树中所有节点,使得每个节点被访问一次且仅被访问一次。
树是一个递归的数据结构,所以可以按照递归您的方式进行遍历。按照对节点访问次序的不同,有4种遍历方式:
- 前序遍历(preorder):根-左-右。在遍历任何一棵子树时,都是先访问根节点,然后递归地前序遍历左子树,最后再递归地前序遍历右子树。
- 中序遍历(inorder):左-根-右。先递归地中序访问左子树,再访问根节点,最后中序访问右子树。
- 后序遍历(postorder):左-右-根。先递归地后序访问左子树,再后续访问右子树,最后访问根节点。
- 层序遍历:从根节点开始,逐层进行遍历,同一层节点则是按照从左至右的顺序依次访问。
2.1 前序遍历
如下图所示,该二叉树的前序遍历顺序为:A - B - D - H - I - E - C - F - J - G - K。
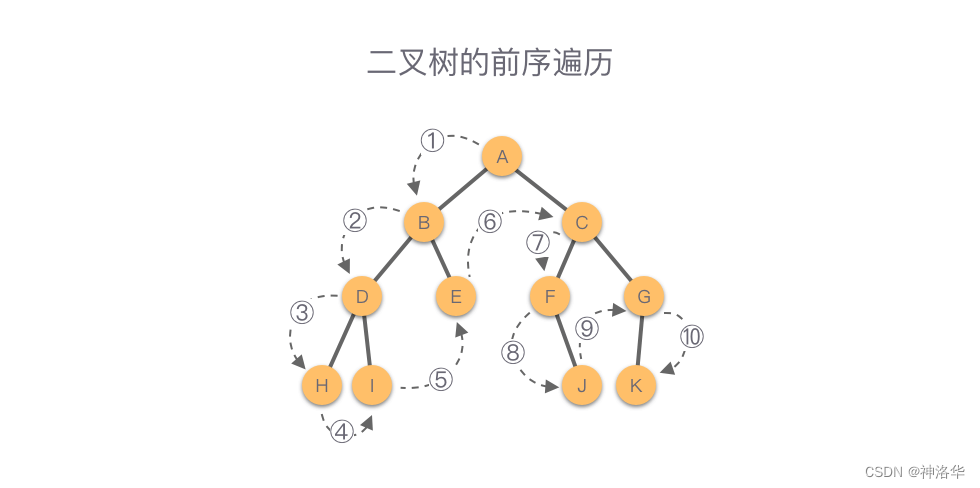
2.1.1 前序遍历的递归实现
前序遍历递归实现代码如下:def preorder(tree):
if tree:
print(tree.getRootVal()) # 访问根节点
preorder(tree.getLeftChild())
preorder(tree.getRightChild())
在前面构造的BinaryTree类里,实现前序遍历,需要加入子树是否为空的判断:
def preorder(self): |
2.1.2 前序遍历的显式栈实现
二叉树的前序遍历递归实现的过程,实际上就是调用系统栈的过程。我们也可以使用一个显式栈 stack 来模拟递归的过程。
前序遍历的顺序为:根节点 - 左子树 - 右子树,而根据栈的「先入后出」特点,所以入栈的顺序应该为:先放入右子树,再放入左子树。这样可以保证最终遍历顺序为前序遍历顺序。 具体实现步骤如下:
- 判断二叉树是否为空,为空则直接返回。
- 初始化维护一个栈,将根节点入栈。
当栈不为空时:
- 弹出栈顶元素
node,并访问该元素。 - 如果
node的右子树不为空,则将node的右子树入栈。 - 如果
node的左子树不为空,则将node的左子树入栈。
二叉树的前序遍历显式栈实现代码如下:
- 弹出栈顶元素
class Solution: |
2.2 中序遍历
遍历任何一棵子树时仍然是按照先遍历子树根节点的左子树,然后访问根节点,最后再遍历子树根节点的右子树的顺序进行遍历。如下图所示,该二叉树的中序遍历顺序为:H - D - I - B - E - A - F - J - C - K - G。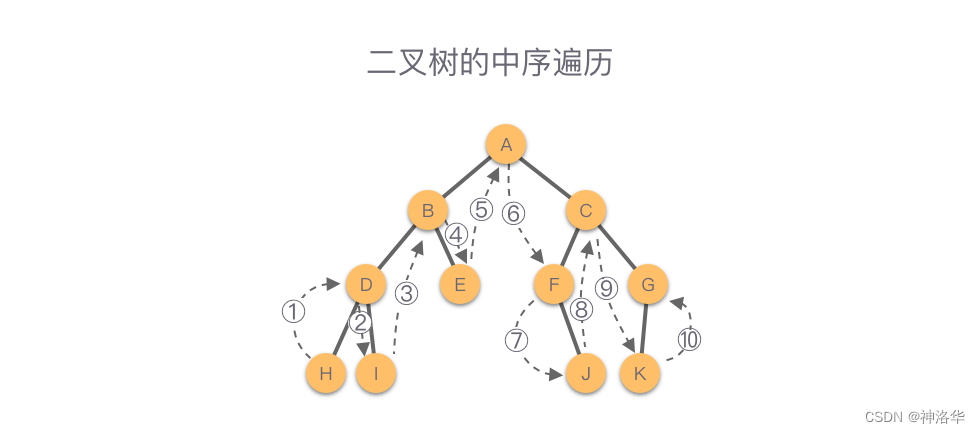
2.2.1 中序遍历的递归实现
def inorder(tree): |
前面1.4 章节根据全括号表达式生成了表达式解析树,反过来也可以用中序遍历的方式,从表达式解析树生成全括号表达式。
# 下面代码对每个数字也加了括号,可以进一步优化 |
2.2.1 中序遍历的显式栈实现
与前序遍历不同,访问根节点要放在左子树遍历完之后。因此我们需要保证:在左子树访问之前,当前节点不能提前出栈。
先从根节点开始,循环遍历左子树,不断将当前子树的根节点放入栈中,直到当前节点无左子树时,从栈中弹出该节点并进行处理。
然后再访问该元素的右子树,并进行上述循环遍历左子树的操作。这样可以保证最终遍历顺序为中序遍历顺序。
二叉树的中序遍历显式栈实现步骤如下:
- 判断二叉树是否为空,为空则直接返回。
- 初始化维护一个空栈。
当根节点或者栈不为空时:
- 如果当前节点不为空,则循环遍历左子树,并不断将当前子树的根节点入栈。
- 如果当前节点为空,说明当前节点无左子树,则弹出栈顶元素
node,并访问该元素,然后尝试访问该节点的右子树。
二叉树的中序遍历显式栈实现代码如下:
class Solution: |
2.3 后序遍历
后序遍历过程也是一个递归过程。在遍历任何一棵子树时,先遍历子树根节点的左子树,然后遍历子树根节点的右子树,最后再访问根节点。如下图所示,该二叉树的后序遍历顺序为:H - I - D - E - B - J - F - K - G - C - A。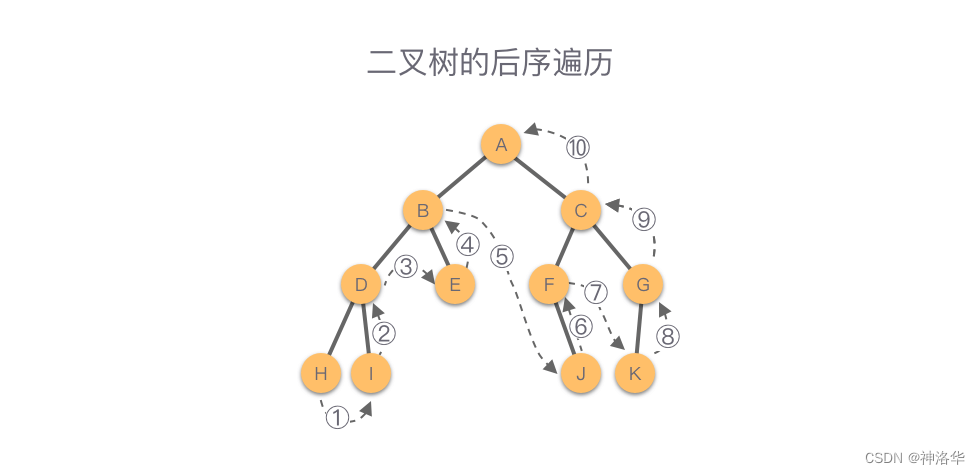
2.3.1 后序遍历的递归实现
def postorder(tree): |
2.3.2 后序遍历的显式栈实现
与前序、中序遍历不同,在后序遍历中,根节点的访问要放在左右子树访问之后。因此,我们要保证:在左右孩子节点访问结束之前,当前节点不能提前出栈。
我们应该从根节点开始,先将根节点放入栈中,然后依次遍历左子树,不断将当前子树的根节点放入栈中,直到遍历到左子树最左侧的那个节点,从栈中弹出该元素,并判断该元素的右子树是否已经访问完毕,如果访问完毕,则访问该元素。如果未访问完毕,则访问该元素的右子树。二叉树的后序遍历显式栈实现步骤如下:
- 判断二叉树是否为空,为空则直接返回。
- 初始化维护一个空栈,使用
prev保存前一个访问的节点,用于确定当前节点的右子树是否访问完毕。 - 当根节点或者栈不为空时,从当前节点开始:
- 如果当前节点有左子树,则不断遍历左子树,并将当前根节点压入栈中。
- 如果当前节点无左子树,则弹出栈顶元素
node。 - 如果栈顶元素
node无右子树(即not node.right)或者右子树已经访问完毕(即node.right == prev),则访问该元素,然后记录前一节点,并将当前节点标记为空节点。 - 如果栈顶元素有右子树,则将栈顶元素重新压入栈中,继续访问栈顶元素的右子树。
class Solution: |
前面1.4章节的表达式解析树求值中,其计算过程其实也是一个后序遍历的过程(左→右→根),所以可以使用后序遍历方法,重写表达式求值代码:
# 后序遍历:表达式求值 |
2.4 层序遍历
层序遍历步骤:
- 如果二叉树为空,则返回。
- 如果二叉树不为空,则:
- 先依次访问二叉树第
1层的节点。 - 然后依次访问二叉树第
2层的节点。 - ……
- 依次下去,最后依次访问二叉树最下面一层的节点。
- 同一层节点则是按照从左至右的顺序依次访问的
- 先依次访问二叉树第
- 如果二叉树不为空,则:
如下图所示,该二叉树的后序遍历顺序为:A - B - C - D - E - F - G - H - I - J - K。
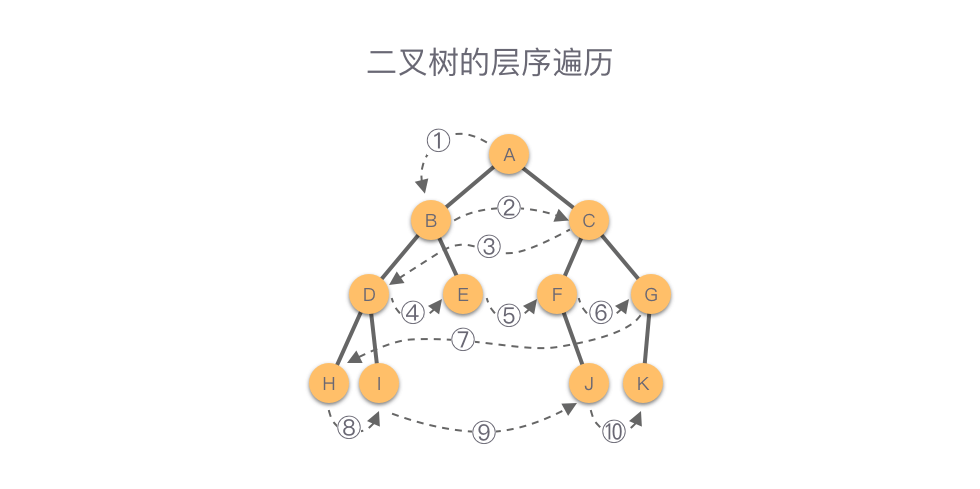
二叉树的层序遍历是通过队列来实现的。具体步骤如下:
- 判断二叉树是否为空,为空则直接返回。
- 令根节点入队。
- 当队列不为空时,求出当前队列长度 $s_i$。
- 依次从队列中取出这 $s_i$ 个元素,并对这 $s_i$ 个元素依次进行访问。然后将其左右子节点入队,然后继续遍历下一层节点。
- 当队列为空时,结束遍历。
二叉树的层序遍历代码实现如下:
class Solution: |
在 while 循环的每一轮中,都是将当前层的所有结点出队列,同时将下一层的所有结点入队列,这样就实现了层序遍历
2.5 二叉树的遍历题目
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 0144 | 二叉树的前序遍历 | Python | 栈、树 | 中等 |
| 0094 | 二叉树的中序遍历 | Python | 栈、树、哈希表 | 简单 |
| 0145 | 二叉树的后序遍历 | Python | 栈、树 | 简单 |
| 0102 | 二叉树的层序遍历 | Python | 树、广度优先搜索 | 中等 |
| 0103 | 二叉树的锯齿形层序遍历 | Python | 树、广度优先搜索、二叉树 | 中等 |
| 0107 | 二叉树的层序遍历 II | Python | 树、广度优先搜索 | 中等 |
| 0104 | 二叉树的最大深度 | Python | 树、深度优先搜索、递归 | 简单 |
| 0111 | 二叉树的最小深度 | Python | 树、深度优先搜索、广度优先搜索 | 简单 |
| 0124 | 二叉树中的最大路径和 | Python | 树、深度优先搜索、动态规划、二叉树 | 困难 |
| 0101 | 对称二叉树 | Python | 树、深度优先搜索、广度优先搜索 | 简单 |
| 0112 | 路径总和 | Python | 树、深度优先搜索 | 简单 |
| 0113 | 路径总和 II | Python | 树、深度优先搜索、回溯、二叉树 | 中等 |
| 0236 | 二叉树的最近公共祖先 | Python | 树 | 中等 |
| 0199 | 二叉树的右视图 | Python | 树、深度优先搜索、广度优先搜索、递归、队列 | 中等 |
| 0226 | 翻转二叉树 | Python | 树、递归 | 简单 |
| 0958 | 二叉树的完全性检验 | Python | 树、广度优先搜索、二叉树 | 中等 |
| 0572 | 另一棵树的子树 | |||
| 0100 | 相同的树 | Python | 树、深度优先搜索 | 简单 |
| 0116 | 填充每个节点的下一个右侧节点指针 | Python | 树、深度优先搜索、广度优先搜索 | 中等 |
| 0117 | 填充每个节点的下一个右侧节点指针 II | Python | 树、深度优先遍历 | 中等 |
| 0297 | 二叉树的序列化与反序列化 | Python | 树、设计 | 困难 |
| 0114 | 二叉树展开为链表 |
2.5.1 二叉树的前序遍历、中序遍历
下面只介绍中序遍历,因为二叉搜索树中用的较多
2.5.1.1 递归
定义 preorderTraversal(self,root) 表示当前遍历到 root 节点的答案。那么按照定义:
- 递归调用self.preorderTraversal(root.left) 来遍历 root 节点的左子树,然后将 root 节点的值加入答案
- 递归调用preorderTraversal(root.right) 来遍历 root 节点的右子树
- 递归终止的条件为碰到空节点。
递归的调用过程是不断往左边走,当左边走不下去了,就打印节点,并转向右边,然后右边继续这个过程。
# Definition for a binary tree node. |
2.5.1.2 迭代
递归实现时,是函数自己调用自己,一层层的嵌套下去,操作系统/虚拟机自动帮我们用 栈 来保存了每个调用的函数,现在我们需要自己模拟这样的调用过程。
class Solution(object): |
或者是:
class Solution(object): |
2.5.2 二叉树的锯齿形层序遍历、二叉树的层序遍历 II
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)
示例:
输入:root = [3,9,20,null,null,15,7] |
此题和 0094 二叉树的中序遍历非常相似,前者都是从左至右遍历每一层。此题只需要将每一层遍历后得到的临时元素列表ls的顺序改变一下,再添加到最终答案ans就行。
class Solution(object): |
如果是 0107二叉树的层序遍历 II ,将ans赋值改一下就行: (如果是ans+=ls,就是正常的自顶向下层序遍历的答案)
''''''# 前面都相同,只是不要level变量 |
2.5.3 二叉树的最大深度、最小深度
1. 二叉树的最大深度
给定一个二叉树,找出其最大深度。示例:
给定二叉树 [3,9,20,null,null,15,7],返回它的最大深度 3 。 |
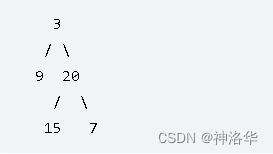
直接套用上面层序遍历的代码,遍历每一层时level+=1,最后返回level。
class Solution(object): |
2. 二叉树的最小深度
给定一个二叉树,找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
输入:root = [2,null,3,null,4,null,5,null,6] |
套用层序遍历模板,当遍历到某一层,有叶节点时(没有左右子节点),返回level。
class Solution(object): |
@[toc]
三、二叉搜索树Binary Search Tree
3.1 二叉搜索树BST的性质
二叉搜索树(二叉查找树):比父节点小的key都出现在左子树,比父节点大的key都出现在右子树,即恒有root.left.val<root.val<root.right.val。
- 中序遍历BST,得到的是升序数组。中序倒序遍历,会得到一个降序数组
最小值一定在根节点的最左下角(中序遍历的起点),最大值一定在根节点的最右下角(中序遍历的终点)
下图是 按照
[70,31,93,94,14,23,73]的顺序插入生成的BST。注意:插入顺序不同,生成的BST也不同。
3.2 二叉搜索树的实现
二叉搜索树可以通过构造TreeNode和BinarySearchTree两个类来实现。
3.2.1 TreeNode类
__iter__:python中使用__iter__方法来实现for循环的迭代。在TreeNode类中重写iter迭代器之后,就可以使用for循环来枚举二叉树中所有的key。- 代码中使用中序遍历的方法实现二叉树的遍历迭代
- 迭代器当中,必须要使用
yield语句,每次调用yield都返回一次迭代之后的返回值(elem)。 - 在
BinarySearchTree中,直接调用TreeNode的__iter__方法进行迭代。
findSuccessor:找到当前节点的后继节点(当前节点的右子树中最小的节点),此方法在BinarySearchTree类的节点删除方法中会调用到。spliceOut:将当前节点摘除(将其子节点直接指向其父节点,跳过当前节点并返回)mytree=BinarySearchTree()
for key,value in mytree:
print(key,value)
class TreeNode: |
3.2.2 BinarySearchTree类
put(key,val)方法:插入key构造BST。- 首先看BST是否为空,如果一个节点都没有,那么key成为根节点root;
- 如果不是空树,就调用一个递归函数
_put(key, val, root)来放置key。
_put(key,val,self.root)的流程:- 如果key比当前节点currentNode小,那么递归_put到左子树。但如果没有左子树,那么key就成为左子节点;
- 如果key比currentNode大,那么递归_put到右子树,但如果没有右子树,那么key就成为右子节点。
- 下图显示在一个BST中插入新的节点19,每次插入操作都是从根节点开始进行比较,灰色表示当前节点。

__setitem__:python内置的索引赋值特殊方法,重写之后可以直接进行索引赋值,例如:
def __setitem__(self, k, v): |
__getitem__:python内置函数,用于索引取值,例如输入mytree[3],可以返回’red’。__contains__:python内置函数,用于调用in函数。in函数对应__contains__方法。get方法:在树中找到key所在的节点并返回它的值。- 如果是空树,直接返回None
- 不是空树,递归地调用
self._get找到节点key。
delete方法:删除节点。- 用
_get方法找到要删除的节点,然后调用remove来删除,找不到则提示错误。 - 从BST中remove一个节点,还要求仍然保持BST的性质,分以下三种情况:这个节点没有子节点;这个节点有1个子节点;这个节点有2个子节点。
- 当前节点是叶节点,则直接删除。判断其是叶节点之后,在判断其是左子节点还是右子节点,然后将其父节点的左子节点或者右子节点指向None就行。
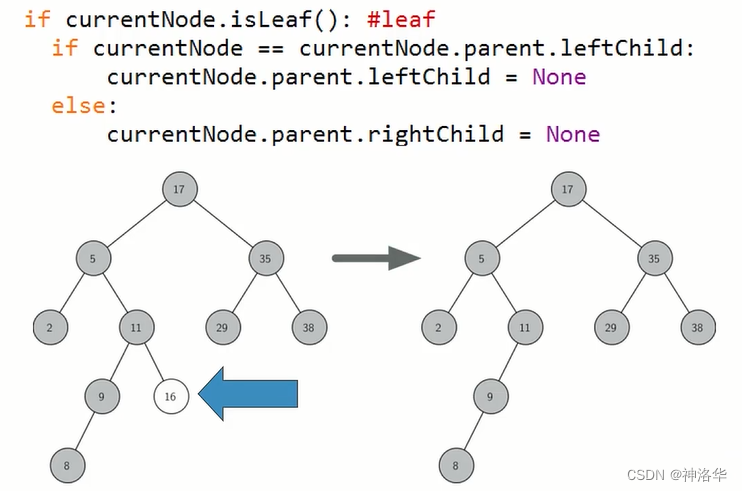
- 当前节点是叶节点,则直接删除。判断其是叶节点之后,在判断其是左子节点还是右子节点,然后将其父节点的左子节点或者右子节点指向None就行。
- 用
2. 被删节点有1个子节点,解决方法:将这个唯一的子节点上移,替换掉被删节点的位置。实际中要分好几种情况。

3. 被删节点有2个子节点。这时无法简单地将某个子节点上移替换被删节点。但可以找到另一个合适地节点来替换被删节点,这个合适节点就是被删节点的下一个key值节点,即**被删节点右子树中最小的那个**,称为**后继节点**。(当前节点右子树中最左下角叶节点)

__delitem__:这是del函数的调用方法,重写之后,可以使用del语句删除节点。
代码实现:
class BinarySearchTree: |
3.3 平衡二叉搜索AVL树
二叉搜索树复杂度分析(以 put 为例)
put操作的性能,决定因素在于二叉搜索树的高度(最大层次),而其高度又受数据项 key 插入顺序的影响。
平衡二叉树能在key插入时一直保持平衡。其代码结构和BST类似,只是生成和维护的过程不一样。
- 平衡二叉树的实现中,需要对每个节点跟踪平衡因子
balance factor。 - 平衡因子是根据节点的左右子树的高度来定义的,确切地说,是左右子树的高度差:
balanceFactor = height(leftSubTree) - height(rightSubTree)。如果平衡因子大于0,称为左重left-heavy,小于零称为右重right-heavy,平衡因子balanceFactor=0,则称作平衡。 - 如果一个二叉搜素树中每个节点的平衡因子都在-1, 0, 1之间,则把这个二叉搜索树称为平衡树。
在平衡树操作过程中,有节点的平衡因子超出此范围,则需要一个重新平衡的过程。
3.3.2 平衡二叉树最差情性能:
AVL树要求平衡因子为1或者-1。下图为平衡因子为1的左重AVL树,树的高度从1开始,来看看问题规模(总节点数N)和比对次数(树的高度h)之间的关系如何。
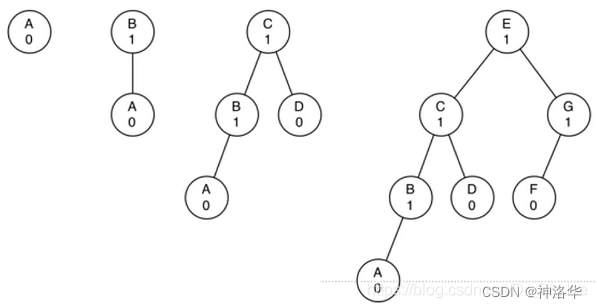
观察上图h = 1~4时,总节点数N的变化:
h = 1, N = 1 |
可得通式:$Nh = 1 + N{h-1} + N_{h-2}$ ,观察这个通式,很接近斐波那契。

3.3.3 保持AVL树的平衡性质
- 首先,作为BST,新key必定以叶节点形式插入到AVL树中。
- 叶节点的平衡因子是0,其本身无需重新平衡,但会影响其父节点的平衡因子:作为左子节点插入,则父节点平衡因子会增加1;作为右子节点插入,则父节点平衡因子会减少1.
- 这种影响可能随着其父节点到根节点的路径一直传递上去,直到:传递到根节点为止;或者某个父节点的平衡因子被调整到0,不再影响上层节点的平衡因子为止。
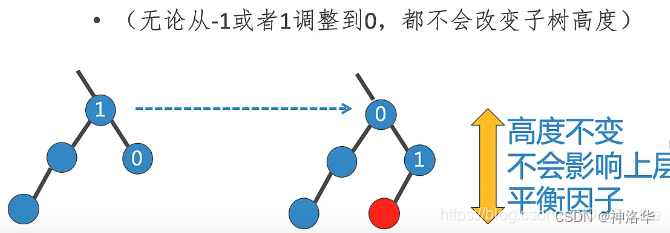
AVL树相比BST只需要调整put方法就行。当插入节点作为左子节点或者右子节点时有个调整平衡因子的过程
- 第一个if:只要节点的平衡因子不在-1到1就要再次调用自己来平衡。
- 如果插入节点是父节点的左子节点就+1,是右子节点就-1
- 最后一个if:如果父节点调整后还不为0就继续往上调整。
- 第一个if:只要节点的平衡因子不在-1到1就要再次调用自己来平衡。


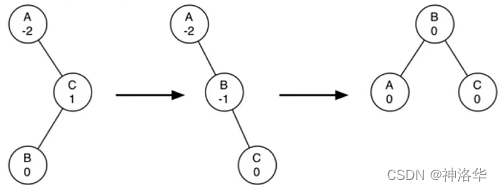
3.3.4 rebalance重新平衡法:左右旋转
主要手段:将不平衡的子树进行旋转
rotation。视左重或者右重进行不同方向的旋转,同时更新相关父节点引用,更新旋转后被影响节点的平衡因子。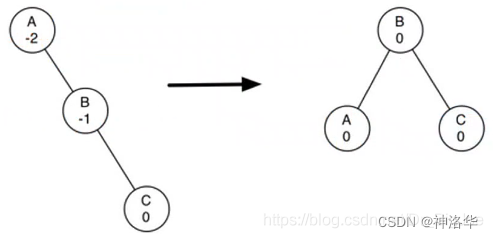
如上图,是一个右重子树A的左旋转(并保持BST性质)。将右子节点B提升为子树的根,将旧根节点A作为新根节点B的左子节点;如果新根节点B原来有左子节点,则将此节点设置为A的右子节点(A的右子节点一定有空)。
- 更复杂的情况:如下图左重的子树右旋转。旋转后,新根节点将旧根节点作为右子节点,但是新根节点原来已有右子节点,需要将原有的右子节点重新定位;原有的右子节点D改到旧根节点E的左子节点,同样,E的左子节点在旋转后一定有空。
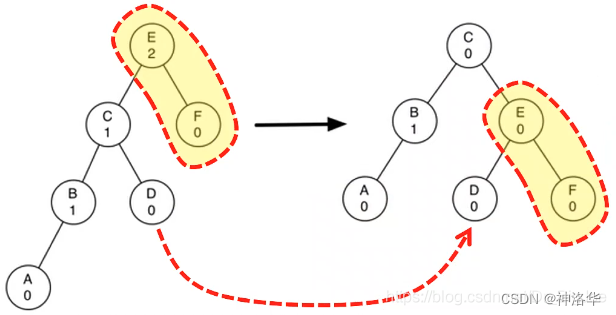
3.3.5 左旋转对平衡因子的影响:
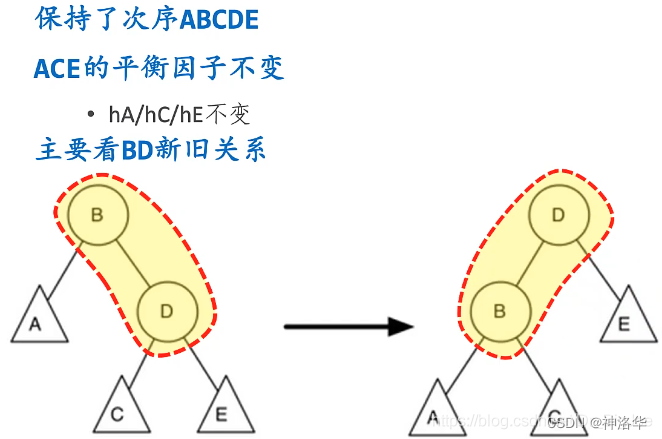
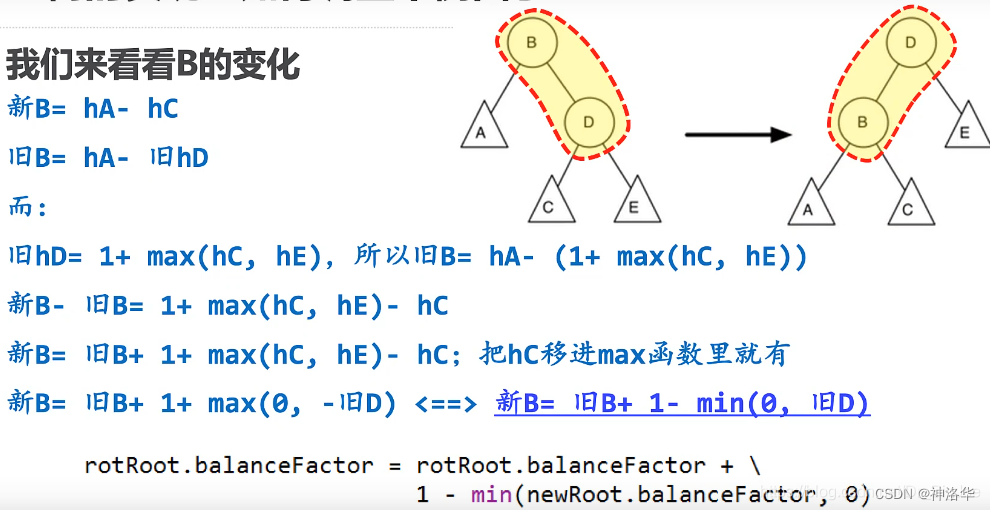
下图右重子树,单纯的左旋转无法实现平衡,左旋转后变成左重了,左重再右旋转,还回到右重。

所以,在左旋转之前检查右子节点的因子,如果右子节点左重的话,先对它进行右旋转,再实施原来的左旋转;同样,在右旋转之前检查左子节点的因子,如果左子节点右重的话,先对它进行左旋转,再实施原来的右旋转。

AVL树算法代价:
- 经过复杂的put方法,AVL树始终维持平衡,get方法也始终保持$O(logn)$高性能。
- 将AVL树的put方法分为两个部分:
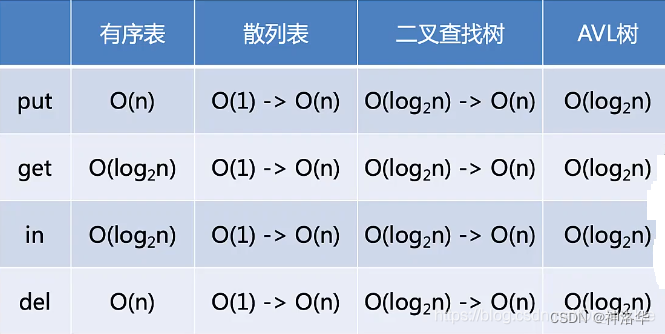
有序表插入需要按顺序找到位置,所以是$O(n)$,查找时可以使用二分查找,所以是$O(logn)$,in和get一样的二分查找。
散列表:根据散列函数计算每个值应该呆的地方,一般情况下是$O(1)$的。因为散列冲突,最坏情况退化到$O(n)$
二叉搜素树:各种操作一般都是$O(logn)$,但是随着插入顺序的而不同,极端情况会退化到线性表$O(n)$
当对内存和计算时间要求不高的时候可以用散列表,其次是AVL数。python内置的字典就是散列表实现的。
四、 二叉搜索树题目
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 0098 | 验证二叉搜索树 | Python | 树、深度优先搜索、递归 | 中等 |
| 0173 | 二叉搜索树迭代器 | Python | 栈、树、设计 | 中等 |
| 0700 | 二叉搜索树中的搜索 | Python | 树 | 简单 |
| 0701 | 二叉搜索树中的插入操作 | Python | 树 | 中等 |
| 0450 | 删除二叉搜索树中的节点 | Python | 树 | 中等 |
| 0703 | 数据流中的第 K 大元素 | Python | 树、设计、二叉搜索树、二叉树、数据流、堆(优先队列) | 简单 |
| 剑指 Offer 54 | 二叉搜索树的第k大节点 | Python | 树、深度优先搜索、二叉搜索树、二叉树 | 简单 |
| 0230 | 二叉搜索树中第K小的元素 | |||
| 0235 | 二叉搜索树的最近公共祖先 | Python | 树 | 简单 |
| 0426 | 将二叉搜索树转化为排序的双向链表 | Python | 栈、树、深度优先搜索、二叉搜索树、链表、二叉树、双向链表 | 中等 |
| 0108 | 将有序数组转换为二叉搜索树 | Python | 树、深度优先搜索 | 简单 |
| 0110 | 平衡二叉树 | Python | 树、深度优先搜索、递归 | 简单 |
4.1 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
- 思路一:中序遍历,看结果是否是升序
根据二叉搜索树的性质可知,中序遍历二叉树,结果一定是升序。
# Definition for a binary tree node. |
- 思路二:递归
class Solution: |
4.2 二叉搜索树迭代器
实现一个二叉搜索树的迭代器 BSTIterator。表示一个按中序遍历二叉搜索树(BST)的迭代器:
def __init__(self, root: TreeNode)::初始化 BSTIterator 类的一个对象,会给出二叉搜索树的根节点。def hasNext(self) -> bool::如果向右指针遍历存在数字,则返回 True,否则返回 False。def next(self) -> int::将指针向右移动,返回指针处的数字。
示例:
输入 |
- 思路一:列表存储
初始化时就逆序遍历二叉搜索树,将结果添加到列表中。当执行next方法时,直接pop列表的最后一个元素
# Definition for a binary tree node. |
思路二:迭代
中序遍历的顺序是:左、根、右。我们使用一个栈来保存节点,以便于迭代的时候取出对应节点。- 初始化的时候,遍历当前节点的左子树,将其路径上的节点存储到栈中。
- 调用
next方法的时候,从栈顶取出节点- 因为之前已经将路径上的左子树全部存入了栈中,所以此时该节点的左子树为空
- 取出该节点的右子树,再将右子树的左子树进行递归遍历,并将其路径上的节点存储到栈中。
- 调用
hasNext的方法的时候,直接判断栈中是否有值即可。class BSTIterator:
def __init__(self, root: TreeNode):
self.stack = []
self.in_order(root)
def in_order(self, node):
while node:
self.stack.append(node)
node = node.left
def next(self) -> int:
node = self.stack.pop()
if node.right:
self.in_order(node.right)
return node.val
def hasNext(self) -> bool:
return len(self.stack)4.3 二叉搜索树中的搜索、插入和删除
- 0070 二叉搜索树中的搜索
- 0701 二叉搜索树中的插入操作
- 0450 删除二叉搜索树中的节点
4.3.1 二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。找到值为val的节点并返回以这个节点为根的子树。 如果节点不存在,则返回 null 。
示例:输入:root = [4,2,7,1,3], val = 2
输出:[2,1,3]class Solution(object):
def searchBST(self, root, val):
"""
:type root: TreeNode
:type val: int
:rtype: TreeNode
"""
if root:
if val<root.val:
return self.searchBST(root.left,val)
elif val>root.val:
return self.searchBST(root.right,val)
else:
return root
else:
return None
4.3.2 二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。
- 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
- 可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
- 示例:
输入:root = [4,2,7,1,3], val = 5
输出:[4,2,7,1,3,5]
结果也可以是:
解题思路:
在二叉搜索树中,对任意节点都有:root.left.val < root.val<root.right.val。所以需要根据 val 和当前节点的大小关系,来确定将 val 插入到当前节点的哪个子树上。
- 如果key比当前节点小,递归地放到其左子树,如果没有左子树,就直接作为其左子节点
- 如果key比当前节点大,递归地放到其右子树,如果没有右子树,就直接作为其右子节点
class Solution(object): |
或者是:
class Solution(object): |
4.3.3 删除二叉树中的节点
给定一个二叉搜索树的根节点 root,以及一个值 key。要求从二叉搜索树中删除 key 对应的节点。并保证删除后的树仍是二叉搜索树。
- 算法时间复杂度为 $0(h)$,$h$ 为树的高度。最后返回二叉搜索树的根节点。
- 示例;
输入:root = [5,3,6,2,4,null,7], key = 3 |
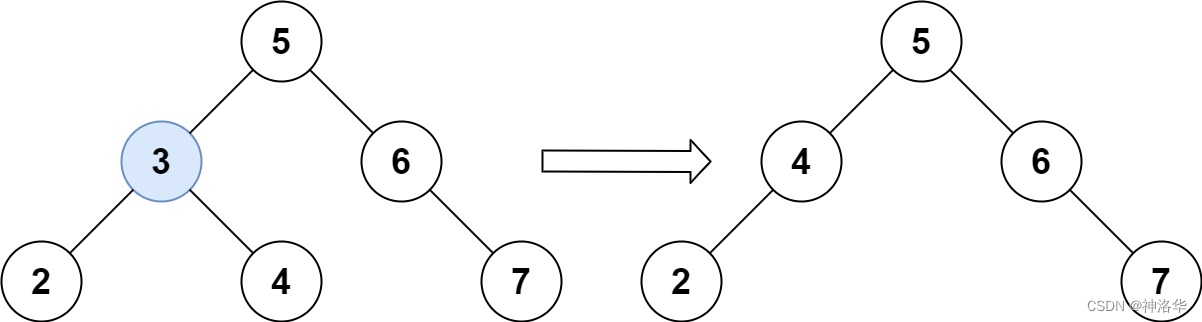
删除分两个步骤:查找和删除。查找通过递归查找,删除的话需要考虑情况。
- 从根节点
root开始,递归遍历搜索二叉树。- 如果当前节点节点为空,返回当前节点。
- 如果当前节点值大于
key,则去左子树中搜索并删除,此时root.left也要跟着递归更新,递归完成后返回当前节点。 - 如果当前节点值小于
key,则去右子树中搜索并删除,此时root.right也要跟着递归更新,递归完成后返回当前节点。 - 如果当前节点值等于
key,则该节点就是待删除节点。- 如果当前节点的左子树为空,则使用其右子树代替当前节点位置,返回右子树。
- 如果当前节点的右子树为空,则使用其左子树代替当前节点位置,返回左子树。
- 如果当前节点的左右子树都有,则将左子树转移到右子树最左侧的叶子节点位置上,相当于被删节点没有了左子树,然后按照没有左子树处理。
class Solution(object): |
4.4 数据流中的第 K 大元素
设计一个 KthLargest 类,用于找到数据流中第 k 大元素。
KthLargest(int k, int[] nums):使用整数 k 和整数流 nums 初始化对象。int add(int val):将 val 插入数据流 nums 后,返回当前数据流中第 k 大的元素。
输入: |
思路:使用最小堆保存前K个最大的元素,堆顶就是第k大的元素
- 建立大小为
k的最小堆,将前K个最大元素压入堆中。 - 每次
add操作时,将新元素压入堆中,如果堆中元素超出了k个,则将堆中最小元素(堆顶)移除,保证堆中元素保证不超过k个。 - 此时堆中最小元素(堆顶)就是整个数据流中的第
k大元素。
- 大顶堆:根节点值 ≥ 子节点值,也叫最大堆
max heap,最大key排在队首。- 小顶堆:根节点值 ≤ 子节点值,也叫最小堆
min heap,最小key排在队首Python heapq库的用法介绍:
- heapq.heapify(list):从列表创建最小堆
- heapq._heapify_max(list):从列表创建最大堆
- heappush(heap, item):将数据item入堆
- heappop(heap):将堆中最小元素出堆(最小的就是堆顶)
- heapq.heapreplace(heap.item) :先操作heappop(heap),再操作heappush(heap,item)。
- heapq.heappushpop(list, item):先操作heappush(heap,item),再操作heappop(heap),和上一个函数相反。
- heapq.merge(*iterables):合并多个堆,例如
a = [2, 4, 6],b = [1, 3, 5],c = heapq.merge(a, b)- heapq.nlargest(n, iterable,[ key]):返回堆中的最大n个元素
- heapq.nsmallest(n, iterable,[ key]):返回堆中最小的n个元素
- heapq[0]:返回堆顶
示例:array = [10, 17, 50, 7, 30, 24, 27, 45, 15, 5, 36, 21]
heapq.heapify(array)
print(heapq.nlargest(2, array))
print(heapq.nsmallest(3, array))
[50, 45]
[5, 7, 10]
代码:class KthLargest(object):
import heapq
def __init__(self, k, nums):
"""
:type k: int
:type nums: List[int]
"""
self.k=k
self.queue=nums
heapq.heapify(self.queue)
print(self.queue)
def add(self, val):
"""
:type val: int
:rtype: int
"""
heapq.heappush(self.queue,val)
while len(self.queue)>self.k:
heapq.heappop(self.queue)
return self.queue[0]
4.5 二叉搜索树的第k大节点
给定一棵二叉搜索树,请找出其中第 k 大的节点的值。
4.5.1 中序递归遍历
- 存储遍历结果,取第n-k个元素的值
class Solution(object):
def __init__(self,ans=None):
self.ans=[]
def kthLargest(self, root, k):
"""
:type root: TreeNode
:type k: int
:rtype: int
"""
ans=self.inorder(root)
return ans[len(ans)-k]
def inorder(self,root):
# 中序遍历
if root:
self.inorder(root.left)
self.ans.append(root.val)
self.inorder(root.right)
return self.ans - 中序的倒序遍历,返回第k个结果
- 终止条件: 当节点 root 为空(越过叶节点),则直接返回;
- 递归右子树: 即 dfs(root.right) ;
- 提前返回: 若 k=0 ,代表已找到目标节点,无需继续遍历,因此直接返回;
- 统计序号: 执行 k=k−1
- k=0 ,代表当前节点为第 k 大的节点,因此记录 res=root.val ;
- 递归左子树: 即 dfs(root.left) ;
class Solution(object): |
直接self.k == 0时,self.res存储结果,再return self.res,会返回空。
4.5.2 迭代
class Solution(object): |
或者是:
class Solution(object): |
4.6 二叉搜索树的最近公共祖先
给定一个二叉搜索树的根节点 root,以及其中两个指定节点 p 和 q,找到该这两个指定节点的最近公共祖先。
说明:
- 祖先:若节点
p在节点node的左子树或右子树中,或者p == node,则称node是p的祖先。 - 最近公共祖先:对于树的两个节点
p、q,最近公共祖先表示为一个节点lca_node,满足lca_node是p、q的祖先且lca_node的深度尽可能大(一个节点也可以是自己的祖先)。 - 所有节点的值都是唯一的。
p、q为不同节点且均存在于给定的二叉搜索树中。- 示例:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
如果是节点 2 和节点 4 ,其最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
对于节点 p、节点 q,最近公共祖先就是从根节点分别到它们路径上的分岔点,也是路径中最后一个相同的节点,现在我们的问题就是求这个分岔点。
我们可以使用递归遍历查找二叉搜索树的最近公共祖先,具体方法如下。
- 从根节点
root开始遍历。 - 如果当前节点的值大于
p、q的值,说明p和q应该在当前节点的左子树,因此将当前节点移动到它的左子节点,继续遍历; - 如果当前节点的值小于
p、q的值,说明p和q应该在当前节点的右子树,因此将当前节点移动到它的右子节点,继续遍历; - 如果当前节点不满足上面两种情况,则说明
p和q分别在当前节点的左右子树上,则当前节点就是分岔点,直接返回该节点即可。
class Solution: |
4.7 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
- 高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
- 示例:
输入:nums = [-10,-3,0,5,9] |

思路 1:递归遍历
直观上,如果把数组的中间元素当做根,那么数组左侧元素都小于根节点,右侧元素都大于根节点,且左右两侧元素个数相同,或最多相差 $1$ 个。那么构建的树高度差也不会超过 $1$。
所以猜想出:如果左右子树越平均,树就越平衡。这样我们就可以每次取中间元素作为当前的根节点,两侧的元素作为左右子树递归建树,左侧区间 $[L, mid - 1]$ 作为左子树,右侧区间 $[mid + 1, R]$ 作为右子树。
class Solution: |
4.8 平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
高度平衡二叉树:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1
思路:递归遍历
- 先递归遍历左右子树,判断左右子树是否平衡,再判断以当前节点为根节点的左右子树是否平衡。
- 如果遍历的子树是平衡的,则返回它的高度,否则返回 -1。
- 只要出现不平衡的子树,则该二叉树一定不是平衡二叉树。
class Solution: |